Sketch the graphs. 2log4x
To sketch the graph of the function y=2log4x, we will follow these steps:
Step 1: Rewrite the Function
We start with the function:
\(
y = 2 \log_4 x
\)
Using the change of base formula and properties of logarithms, we can rewrite this as:
\(
y = 2 \cdot \frac{\log_2 x}{\log_2 4}
\)
Since \( \log_2 4 = 2 \), we can simplify:
\(
y = 2 \cdot \frac{\log_2 x}{2} = \log_2 x
\)
Step 2: Determine the Domain
The logarithmic function \( \log_2 x \) is defined only for \( x > 0 \). Therefore, the domain of the function \( y = 2 \log_4 x \) is:
\(
x > 0
\)
Step 3: Identify Key Points
Now, we will find some key points to help us sketch the graph:
1. When \( x = 1 \):
\(
y = \log_2 1 = 0
\)
So, the point \( (1, 0) \) is on the graph.
2. When \( x = 2 \):
\(
y = \log_2 2 = 1
\)
So, the point \( (2, 1) \) is on the graph.
3. As \( x \) approaches \( 0 \) (from the right), \( y \) approaches \( -\infty \):
\(
\lim_{x \to 0^+} y = -\infty
\)
4. As \( x \) approaches \( \infty \), \( y \) also approaches \( \infty \):
\(
\lim_{x \to \infty} y = \infty
\)
Step 4: Sketch the Graph
Now we can sketch the graph using the information we have gathered:
- The graph will start from \( (-\infty, -\infty) \) as \( x \) approaches \( 0 \).
- It will pass through the point \( (1, 0) \).
- It will also pass through the point \( (2, 1) \).
- The graph will continue to rise and approach \( \infty \) as \( x \) approaches \( \infty \).
Final Graph
The graph of \( y = 2 \log_4 x \) (which is equivalent to \( y = \log_2 x \)) will look like this:
y∣∣|/||/|/∣∣|/|/|/||/|∠__________x
We start with the function:
\(
y = 2 \log_4 x
\)
Using the change of base formula and properties of logarithms, we can rewrite this as:
\(
y = 2 \cdot \frac{\log_2 x}{\log_2 4}
\)
Since \( \log_2 4 = 2 \), we can simplify:
\(
y = 2 \cdot \frac{\log_2 x}{2} = \log_2 x
\)
The logarithmic function \( \log_2 x \) is defined only for \( x > 0 \). Therefore, the domain of the function \( y = 2 \log_4 x \) is:
\(
x > 0
\)
Now, we will find some key points to help us sketch the graph:
1. When \( x = 1 \):
\(
y = \log_2 1 = 0
\)
So, the point \( (1, 0) \) is on the graph.
2. When \( x = 2 \):
\(
y = \log_2 2 = 1
\)
So, the point \( (2, 1) \) is on the graph.
\(
\lim_{x \to 0^+} y = -\infty
\)
\(
\lim_{x \to \infty} y = \infty
\)
Now we can sketch the graph using the information we have gathered:
- The graph will start from \( (-\infty, -\infty) \) as \( x \) approaches \( 0 \).
- It will pass through the point \( (1, 0) \).
- It will also pass through the point \( (2, 1) \).
- The graph will continue to rise and approach \( \infty \) as \( x \) approaches \( \infty \).
The graph of \( y = 2 \log_4 x \) (which is equivalent to \( y = \log_2 x \)) will look like this:
Topper's Solved these Questions
- RELATIONS AND FUNCTIONSBOOK - ICSECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - EXERCISE 2 (f)
29 Videos
- RELATION AND FUNCTIONSBOOK - ICSECHAPTER - RELATION AND FUNCTIONSEXERCISE - MULTIPLE CHOICE QUESTIONS (Choose the correct answer from the given four options in questions)
32 Videos
- SAMPLE QUESTION PAPER 01BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER 01EXERCISE - SECTION C
8 Videos
Similar Questions
Sketch the graphs. log4x
View SolutionSketch the graphs. 3log4x
View SolutionSketch the graphs. y=log2x
View SolutionSketch the graphs. y=log2(x+1)
View SolutionSketch the graphs. y=log2x+1
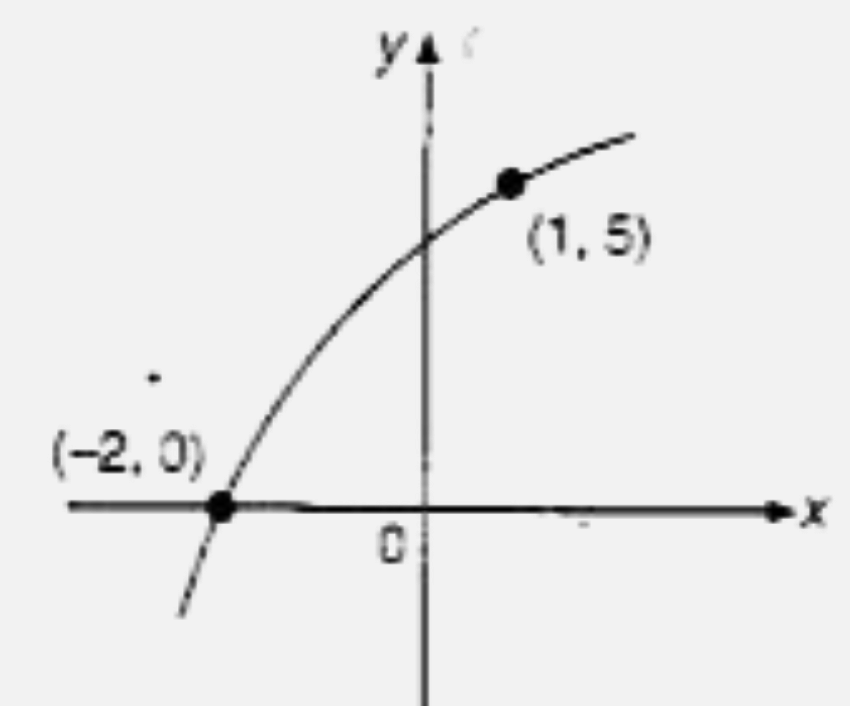
View SolutionA sketch of the graph y=alog4(x+b) is shown. Find the values of a and b.
View SolutionSketch the graph of y=3x
View SolutionSketch the graph of y=log0.5|x|.
View SolutionSketch the graph of cos 4x.
View SolutionSketch the graphs y=2 and y=log102x on the same diagram.
View Solution
