From your graph estimate log41.25
To estimate the value of log4(1.25), we can follow these steps:
Step 1: Understand the logarithmic function
We know that the logarithmic function loga(b) gives us the exponent to which the base a must be raised to produce the number b. In our case, we need to find the exponent y such that:
4y=1.25
Step 2: Identify known values
To estimate log4(1.25), we can use some known values of logarithms:
- log4(1)=0 because 40=1
- log4(4)=1 because 41=4
- log4(16)=2 because 42=16
Step 3: Create a table of values
We can create a table of values for x and y to help us visualize the logarithmic function:
| x | y=log4(x) |
|-----------|------------------------|
| 1 | 0 |
| 4 | 1 |
| 16 | 2 |
| 14 | -1 |
| 116 | -2 |
Step 4: Plot the points and draw the graph
Using the values from the table, we can plot the points on a graph with x on the horizontal axis and y on the vertical axis. The graph will show a curve that approaches the vertical line x=0 (asymptote) but never touches it.
Step 5: Estimate log4(1.25)
From the graph, we can estimate the value of log4(1.25). Since 1.25 is between 1 and 4, we know that log4(1.25) will be between 0 and 1. By observing the graph, we can see that:
log4(1.25)≈0.1609
Final Answer
Thus, the estimated value of log4(1.25) is:
log4(1.25)≈0.1609
---
We know that the logarithmic function loga(b) gives us the exponent to which the base a must be raised to produce the number b. In our case, we need to find the exponent y such that:
4y=1.25
To estimate log4(1.25), we can use some known values of logarithms:
- log4(1)=0 because 40=1
- log4(4)=1 because 41=4
- log4(16)=2 because 42=16
We can create a table of values for x and y to help us visualize the logarithmic function:
|-----------|------------------------|
| 1 | 0 |
| 4 | 1 |
| 16 | 2 |
| 14 | -1 |
| 116 | -2 |
Using the values from the table, we can plot the points on a graph with x on the horizontal axis and y on the vertical axis. The graph will show a curve that approaches the vertical line x=0 (asymptote) but never touches it.
From the graph, we can estimate the value of log4(1.25). Since 1.25 is between 1 and 4, we know that log4(1.25) will be between 0 and 1. By observing the graph, we can see that:
log4(1.25)≈0.1609
Thus, the estimated value of log4(1.25) is:
log4(1.25)≈0.1609
Topper's Solved these Questions
- RELATIONS AND FUNCTIONSBOOK - ICSECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - EXERCISE 2 (f)
29 Videos
- RELATION AND FUNCTIONSBOOK - ICSECHAPTER - RELATION AND FUNCTIONSEXERCISE - MULTIPLE CHOICE QUESTIONS (Choose the correct answer from the given four options in questions)
32 Videos
- SAMPLE QUESTION PAPER 01BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER 01EXERCISE - SECTION C
8 Videos
Similar Questions
Use the table given below to draw the graph.
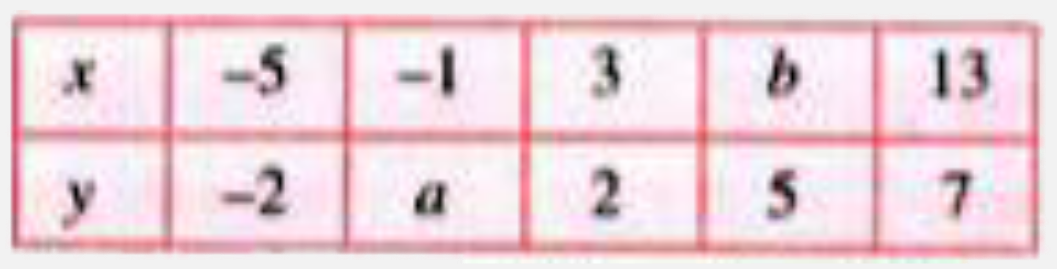
From your graph, find the values of a and b State a linear relation between the vairables x and y.
View SolutionSketch the graphs. log4x
View SolutionDraw a V-I graph for a conductor at two different temperatures. What conclusion do you draw from your graph for the variation of resistance of the conductor with temperature ?
View SolutionSketch the graphs. 2log4x
View SolutionSketch the graphs. 3log4x
View SolutionDraw the graph of y=log2x.
View SolutionDraw the graph of y=−logex.
View SolutionDraw a Histogram for the data, using a graph paper:
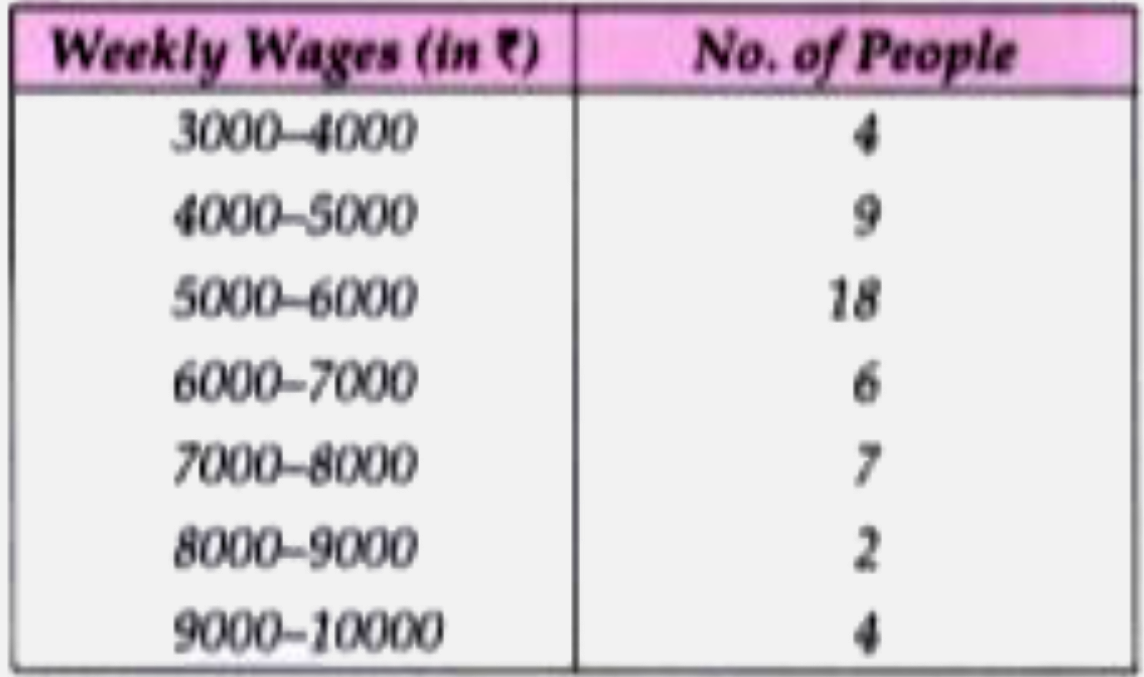
Estimate the mode from the graph.
View SolutionDraw the graph of y=1logex
View SolutionDraw the graph of y=loge(−x),−logex,y=|logex|,y=loge|x| and y=|loge|x|| transforming the graph of y=logex.
View Solution
