What should be the angle at which a swimmer should swim to reach point C from point A (Fig.) ? The speed of the swimmer v, the speed of the stream u, and the angleβ are all known.
The correct Answer is:α=β−arc sinncosβv.
The swimmer swims at an angle α to the y-axis. His speed along the y-axis is vy=vcosα, along the x-axis vx=vsinα+u. Hence
tanβ=vxvy=vsinα+uvcosα
The given answer is obtained after some simple transforms.
The problem has a solution for v≥ucosβ.
Similar Questions
At what angle to the stream should a swimmer swim to reach the opposite bank as soon as possible?
View SolutionA river is flowing from west to east direction with velocity v. A swimmer standing at the south bank wants to cross the river in order to reach a point just in front of the starting point. If the swimmer can swim at a speed of u w.r.t. the river flow, the angle with the north direction, required to swim is equal to?
View Solution
Knowledge Check
A swimmer crosses a river with minimum possible time 10 Second. And when he reaches the other end starts swimming in the direction towards the point from where he started swimming. Keeping the direction fixed the swimmer crosses the river in 15 sec. The ratio of speed of swimmer with respect to water and the speed of river flow is (Assume contant speed of river & swimmer)
A32B94C2√5D√52A swimmer wands to cross a river and reach point B directly from A. The speed of the wimmer in still river and that of river flow are same. The dotted line AN is normal to flow direction of river. For swimmer to reach point B, the angle his velocity relative to river will make with line AN is given by θ. then the value of θ is :
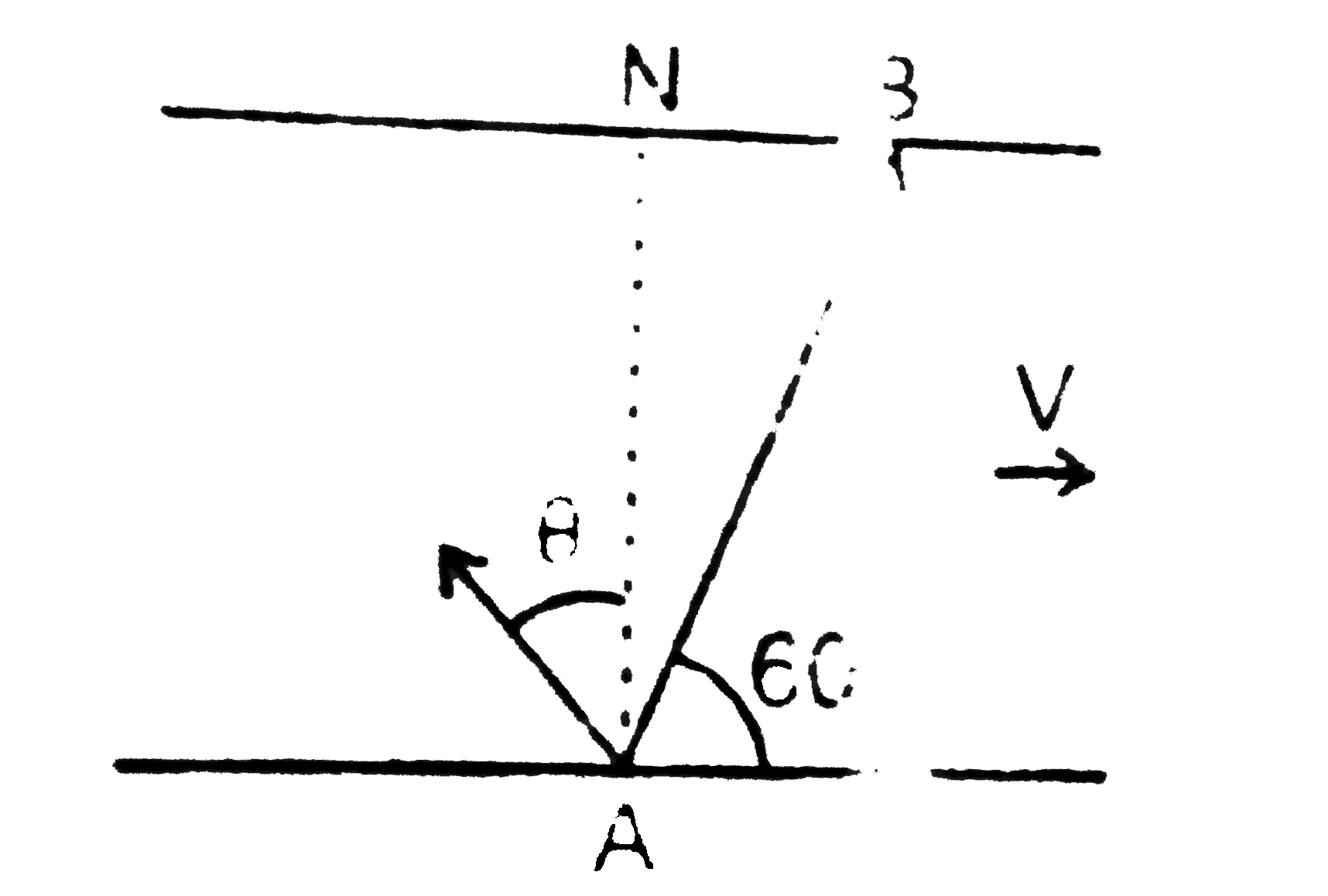 A60∘B30∘C45∘D0∘
A60∘B30∘C45∘D0∘To cross the river in shortest distance, a swimmer should swimming an angle theta with the upsteram. What is the ratio of the time taken to swim across in the shortest time to that in swimming across over shortest distance. [Asume that the speed of swimmer in still water is greater than the speed of river flow]
AcosθBsinθCtanθDcotθ
A swimmer S is in the sea at a distance dkm from the closest point A on a straight shore. The house of the swimmer is on the shore at distance Lkm from A. He can swin at speed oh ukm/h. walk at speed at vkm/h. At what point on shore should he land so that hhe reaches his house in the shortest time.
View SolutionA swimmer wants to directly reach the point B starting from A. The river is flowing along x-axis. If the velocity of the swimmer is √23 times the velocity of the river, find the angle θ from the line AB at which his swimming effort should be directed.
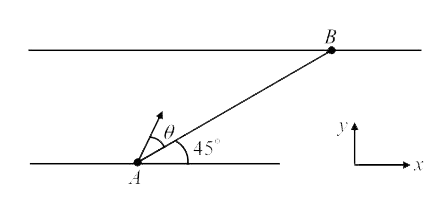
View SolutionA swimmer crosses a river with minimum possible time 10 Second. And when he reaches the other end starts swimming in the direction towards the point from where he started swimming. Keeping the direction fixed the swimmer crosses the river in 15 sec. The ratio of speed of swimmer with respect to water and the speed of river flow is (Assume contant speed of river & swimmer)
View SolutionA swimmer wands to cross a river and reach point B directly from A. The speed of the wimmer in still river and that of river flow are same. The dotted line AN is normal to flow direction of river. For swimmer to reach point B, the angle his velocity relative to river will make with line AN is given by θ. then the value of θ is :

View SolutionThe speed of a swimmer with respect to the water is v, the speed of the stream is u. In what direction should the swimmer move to reach the opposite point on the other bank of the river? How long will he swim if the width of the river is l?
View Solution
