Find the position of the centre of two unequal antiparallel forces. The distance between the points of application of the forces F1 and F2 is a.
The correct Answer is:d=F2a/(F1−F2)
Resolve the greater force F1 into two parallel components (Fig.), applying the force T2=−F2 at the point A2 and the second force T1 of magnitude T1=F1−F2 at the point C at a distance

d=aT2/T1 from point A1. Since the forces F2 and T2 are in equilibrium, the resultant R=T1, its magnitude is R=T1=F1−F2.
Similar Questions
A thin uniform rod AB of mass 1 kg moves translationally with acceleration a=2m/s2 due to two antiparallel forces F1 & F2. The distance between the points at which these forces are applied is equal to l=0.2m. If force F−(1)=8N then find the length of the rod in meter

View SolutionTwo parallel forces F1 and F2 acting in the same direction are applied to a rigid body.
Porve that
(a) the magnitude of the resultant force is equal to the sum of magnitudes of the forces being added,
(b) the resultant force is parallel to the forces being added and acts in the same direction,
(c ) the resultant force passes through the centre of the parallel forces, i.e. through the point which divides the distance between the points of application of both forces into sections inversely proportional to the magnitude of the forces.
View Solution
Knowledge Check
A thin uniform rod AB of mass 1 kg moves translationally with acceleration a=2m/s2 due to two antiparallel forces F1 & F2. The distance between the points at which these forces are applied is equal to l=0.2m. If force F−(1)=8N then find the length of the rod in meter
 A1 mB2 mC3 mD4 m
A1 mB2 mC3 mD4 m
In the given figure, thin uniform rod AB of mass kg moves translationally with acceleration a=2ms^(2)due→twoantiparal≤lforcesF_(1) ,F_(2).Thedistancebetweenthep∮satwhichtheseforcesareappliedisequal→0.2 m.IfforceF_(1)=8 N, then find the length of the rod in meter.
'(##CEN_KSR_PHY_JEE_C09_E01_022_Q11##)'
View SolutionA Thin uniform rod AB of mass m=1.0kg moves translationally with acceleration a=2.0m/s2 due to two antiparallel forces F1 and F2. The distance between the points at which these forces are applied is equal to d=20cm. Besides, it is known that F2=5.0N. Find the length of the rod.

View SolutionA thin uniform rod AB of mass m=1.0kg moves translationally with acceleration w=2.0m/s2 due to two antiparallel forces F1 and F2 (figure). The distance between the points at which these forces are applied is equal to a=20cm. Besides, it is known that F2=5.0N. Find the length of the rod.
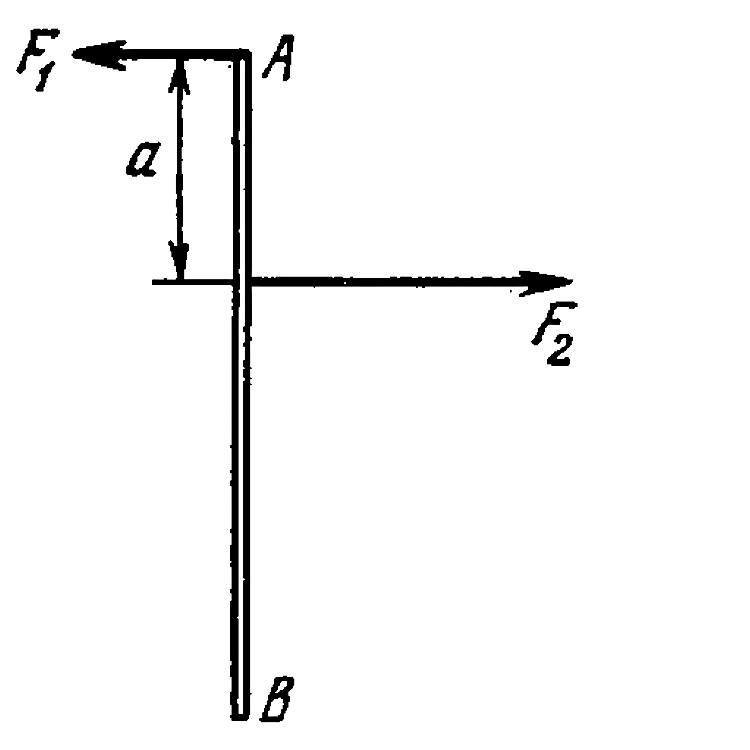
View SolutionA force couple is the term used for a system of two equal antiparallel forces, the arm of the couple is the shortest distance between the forces. Prove that the torque is equal to the product of the magnitude of the force and the arm no matter what is the position of the point with respect to which the torque is determined.
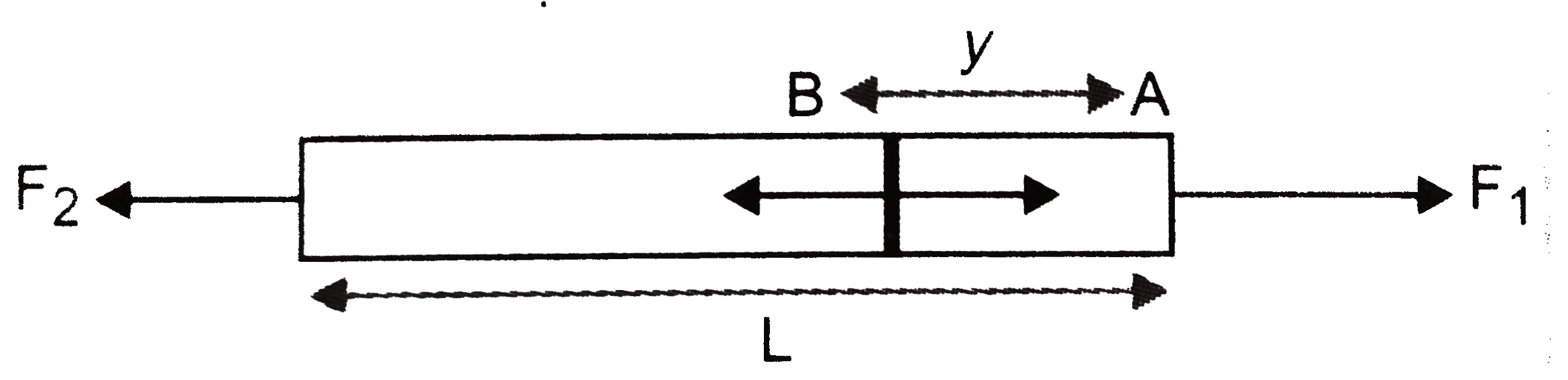
View SolutionWhat is the tension in a rod of length length L and mass M at a distance y fromF1 when the rod is acted on by two unequal force F1 and F2(<F1) as shown in.
View SolutionThere are four force acting at a point p produced by strings as shown in figure, which is at rest. The force F1 and F2 are .

View SolutionFind the torque of a force F=a(ˆi+2ˆj+3ˆk) N about a point O. The position vector of point of application of force about O is r=(2ˆi+3ˆj−ˆk) m.
View Solution
