A weight of mass m is suspended from a cord so that one section of it makes an angle alph1 with the horizontal and the other - an angle α2 (Fig.). Find the tension of these sections of the cord.

The correct Answer is:T1=Pcosα2sin(α1+α2),T2=Pcosα1sinα1+α2
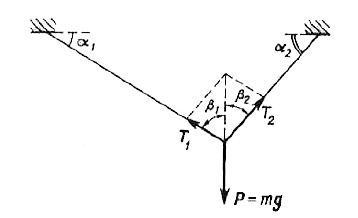
Using the sine rule, we obtain from Fig.
T1sinβ2=T2sinβ1=Psin[π (β1|β2)]
Noting that β1=π2−α1,β2=π2−α2, we obtain the given answer.
Similar Questions
Knowledge Check
A mass of 10 kg is suspended from a spring balance, it is pulled aside by a horizontal string so that it makes an angle 60∘ with the vertical. The new reading of the balance is:
A10√3 kg wtB20√3 kg wtC20 kg wtD10 kg wtA mass of 10 kg is suspended from a spring balance. It is pulled aside by a horizontal string so that it makes an angle of 60∘ with the vertical. The new rading of the balance is
A20 kg-wtB10 kg-wtC10√3 kg-wtD20√3 kg-wt
A block of mass M si suspended by two strings angles θ1 and θ2 with the horizontal. Find the tensions in the strings.

View SolutionA weight of mass m hangs on a thread. The thread is deflected by an angle α0 and let go. Find the tension of the thread as a function of the angle α .
View SolutionA weight of mass m is suspended from a hinged bracket (Fig.).
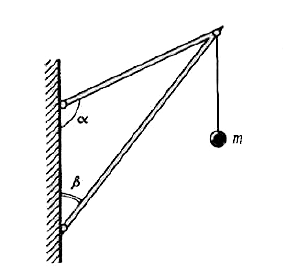
Find the forces in the rods making up the bracket.
View SolutionA bead of mass 2.5×10−4 kg is suspended from a cord. A steady horizontal breeze pushes the bead so that the cord makes a constant angle of 40∘ with the vertical. Find (a) the tension in the cord and (b) the push magnitude.
View SolutionA block of mass M lies on a plane inclined at an angle α to the horizontal. A wieght a mass m is connected to the block by a thread slung over a pulley (Fig.).
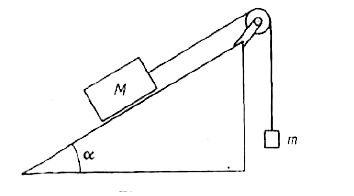
Find the acceleration of the weight and the tension of the thread. Friction, the mass of the pulley and of the thread are to be neglected.
View SolutionA mass of 10 kg is suspended from a spring balance. It is pulled aside by a horizontal string so that it makes an angle of 60∘ with the vertical. The new rading of the balance is
View Solution
