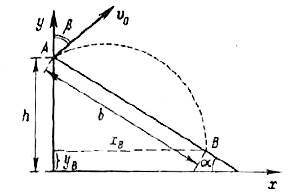
The surface of a hill is inclined at an angle $α$ to the horizontal (Fig.). A stone is thrown from the summit of the hill at an initial speed $v_{0}$ at an angle $β$ to the vertical. How far from the summit will the stone strike the ground?

Text Solution

Verified by Experts

The correct Answer is: $b = \frac{2 v_{0}^{2} sin β cos (α - β)}{g {cos}^{2} α}$

The law of motion of the stone is
$y = h + v_{0} t cos β$ -
$- \frac{1}{2} g t^{2}, x = v_{0} t sin β$
When the stone strikes the hill,
$x_{B} = b cos α, y_{B} = h - b sin α$
Substituting this into the law of motion we obtain the result sought.

|

Updated on:21/07/2023

Class 12 PHYSICS RIGID BODY DYNAMICS

Similar Questions

Knowledge Check

Question 1 - Select One
A ball is projected horizontally with a speed v from the top of the plane inclined at an angle $45^{\circ}$ with the horizontal. How far from the point of projection will the ball strikes the plane?
A $\frac{2 v^{2}}{g}$
B $\sqrt{2} [\frac{2 v^{2}}{g}]$
C $\frac{v^{2}}{g}$
D $\sqrt{2} \frac{v^{2}}{g}$
Question 2 - Select One
A shot is fired at an angle $α$ to the horizontal up a hill of inclination $β$ to the horizontal. Then it strikes the hill horizontally if
A $tan α = 2 tan β$
B $tan α = tan β$
C $tan α . tan β = 1$
DNone

Recommended Questions

Home
Ask Doubt
Profile