Prove that the surface of a liquid in a rotating vessel assumes the form of a paraboloid of rotation.
The correct Answer is:Hint Introduce a rotating frame of reference and use the result of Promlem 3.14
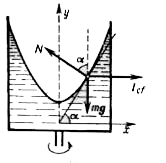
Fix the reference frame to the rotating liquid. Then there will be three forces acting on every particle: the force of gravity mg, the reaction of the liquid N and the centrifugal force of inertia lct==mω2x (Fig. 15.9). The angle between the reaction and the y-axis is equal to the angle between the tangent and the x-axis (since the edges of the angles are mutually perpendicular). We have
tanα=Ictmg=ω2rg
It was shown in Problem 3.14 that the tangent .to a parabola x2==2py makes an angle of tan α=x/p with the z-axis. Therefore we may conclude that the surface of a liquid in a rotating vessel is a paraboloid formed by the parabola x2=2gω2y rotating about the y - axis.
Similar Questions
Knowledge Check
Following eclipsed form of propane is repeated after rotation of:
 A60∘B120∘C180∘D360∘
A60∘B120∘C180∘D360∘A liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the sides. If the radius of the vessel is r and the speed of revolution is n rotations/second, find the difference in height of the liquid at the centre of vessel and its sides.
Ah=2π2n2r2gBh=4π2n2r2gCh=π2r2n2gDh=π2r2n2gA liquid is kept in a cylindrical vessel which is being rotated about a vertical axis through the centre of the circular base. If the radius of the vessel is r and angular velocity of rotation is ω, then the difference in the heights of the liquid at the centre of the vessel and the edge is.
Arω2gBr2ω22gC√2grωDω22gr2
A liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the sides. If the radius of the vessel is r and the speed of revolution is n rotations/second, find the difference in height of the liquid at the centre of vessel and its sides.
View SolutionPressure In Case Of Accelerated Fluids|Rotating Vessel|Questions
View SolutionA liquid is kept in a cylindrical vessel which is being rotated about a vertical axis through the centre of the circular base. If the radius of the vessel is r and angular velocity of rotation is ω, then the difference in the heights of the liquid at the centre of the vessel and the edge is.
View SolutionThe rotation rate of a mixing blade, in rotations per second, slows as a liquid is being added to the mixer. The blade rotates at 1,000 rotations per second when the mixer is empty. The rate at which the blade slows is four rotations per second less than three times the square of the height of the liquid. If h is the height of liquid in the mixer, which of the following represents R(h), the rate of rotation?
View SolutionThree particles, each of mass m are placed an the points (x1,y1,z1),(x2,y2,z2) and (x3,y3,z3) on the inner surface of a paraboloid of revolution obtained by rotating the parabola x2=4ay about the y-axis. Neglected the mass of the paraboloid. (y-axis. is along the vertical (a) the moment of inertia of the system about the axis of the paraboloid is I=4ma(y1+y2+y3)
View Solution
