A liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the sides. If the radius of the vessel is r and the speed of revolution is n rotations/second, find the difference in height of the liquid at the centre of vessel and its sides.
h=2π2n2r2g
h=4π2n2r2g
h=π2r2n2g
h=π2r2n2g
The correct Answer is:A
To solve the problem of finding the difference in height of the liquid at the center of a cylindrical vessel and its sides when the vessel is rotated, we can follow these steps:
1. Understand the System:
- We have a cylindrical vessel of radius r that is rotating about its axis at a speed of n rotations per second.
- The liquid inside the vessel will experience a centrifugal force due to the rotation, causing it to rise at the sides of the vessel.
2. Convert Rotational Speed to Angular Speed:
- The angular speed ω in radians per second can be calculated from the rotational speed n:
ω=2πn(since one rotation is 2π radians)
3. Consider the Pressure Variation:
- The pressure at a point in the liquid at a distance x from the axis of rotation can be expressed considering the centrifugal force. The pressure at the center (point O) is atmospheric pressure Patm.
- As we move outward to a point at distance x, the pressure increases due to the centrifugal effect.
4. Set Up the Pressure Equation:
- For a small height dy at distance x, the pressure at that point can be expressed as:
PB=Patm+ρω2xdx−ρgdy
- Here, ρ is the density of the liquid, g is the acceleration due to gravity, and dy is the small height change.
5. Apply Hydrostatic Equilibrium:
- In hydrostatic equilibrium, the change in pressure must equal zero:
ρω2xdx−ρgdy=0
- This leads to:
ω2xdx=gdy
6. Integrate to Find Height Change:
- Rearranging gives:
dy=ω2xgdx
- Integrate both sides from the center (0) to the radius r:
∫h0dy=∫r0ω2xgdx
- The left side integrates to h, and the right side can be calculated:
h=ω2g⋅(x22)r0=ω2r22g
7. Substitute for Angular Speed:
- Substitute ω=2πn:
h=(2πn)2r22g=4π2n2r22g=2π2n2r2g
8. Determine Height Difference:
- The height at the center of the vessel is 0, and at the sides, it is h. Therefore, the difference in height Δh is:
Δh=h−0=2π2n2r2g
Final Answer:
The difference in height of the liquid at the center of the vessel and its sides is:
Δh=2π2n2r2g
- We have a cylindrical vessel of radius r that is rotating about its axis at a speed of n rotations per second.
- The liquid inside the vessel will experience a centrifugal force due to the rotation, causing it to rise at the sides of the vessel.
- The angular speed ω in radians per second can be calculated from the rotational speed n:
ω=2πn(since one rotation is 2π radians)
- The pressure at a point in the liquid at a distance x from the axis of rotation can be expressed considering the centrifugal force. The pressure at the center (point O) is atmospheric pressure Patm.
- As we move outward to a point at distance x, the pressure increases due to the centrifugal effect.
- For a small height dy at distance x, the pressure at that point can be expressed as:
PB=Patm+ρω2xdx−ρgdy
- Here, ρ is the density of the liquid, g is the acceleration due to gravity, and dy is the small height change.
- In hydrostatic equilibrium, the change in pressure must equal zero:
ρω2xdx−ρgdy=0
- This leads to:
ω2xdx=gdy
- Rearranging gives:
dy=ω2xgdx
- Integrate both sides from the center (0) to the radius r:
∫h0dy=∫r0ω2xgdx
- The left side integrates to h, and the right side can be calculated:
h=ω2g⋅(x22)r0=ω2r22g
- Substitute ω=2πn:
h=(2πn)2r22g=4π2n2r22g=2π2n2r2g
- The height at the center of the vessel is 0, and at the sides, it is h. Therefore, the difference in height Δh is:
Δh=h−0=2π2n2r2g
The difference in height of the liquid at the center of the vessel and its sides is:
Δh=2π2n2r2g
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Multipe Correct
15 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Assertion-Reasoning
8 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Subjective
25 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Video
Similar Questions
A liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the side. If the radius of the vessel is 5cm and the speed of rotation is 4rev/s, then the difference in the height of the liquid at the centre of the vessel and its sides is
View SolutionA liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the side. If the radius of the vessel is 5cm and the speed of rotation is 4rev/s, then the difference in the height of the liquid at the centre of the vessel and its sides is
View SolutionA liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the sides, if the radius of vessel is 0.05m and the speed of rotation is 2rev/s, find difference in the height of the liquid at the centre of the vessel and its sides.
View SolutionA cylindrical vessel containing a liquid is rotated about its axis so that the liquid rises at its sides as shown in the figure . The radius of vessel is 5 cm and the angular speed of rotation is ω rad s−1. The difference in the height , h ( in cm ) of liquid at the centre of vessel and at the side will be :
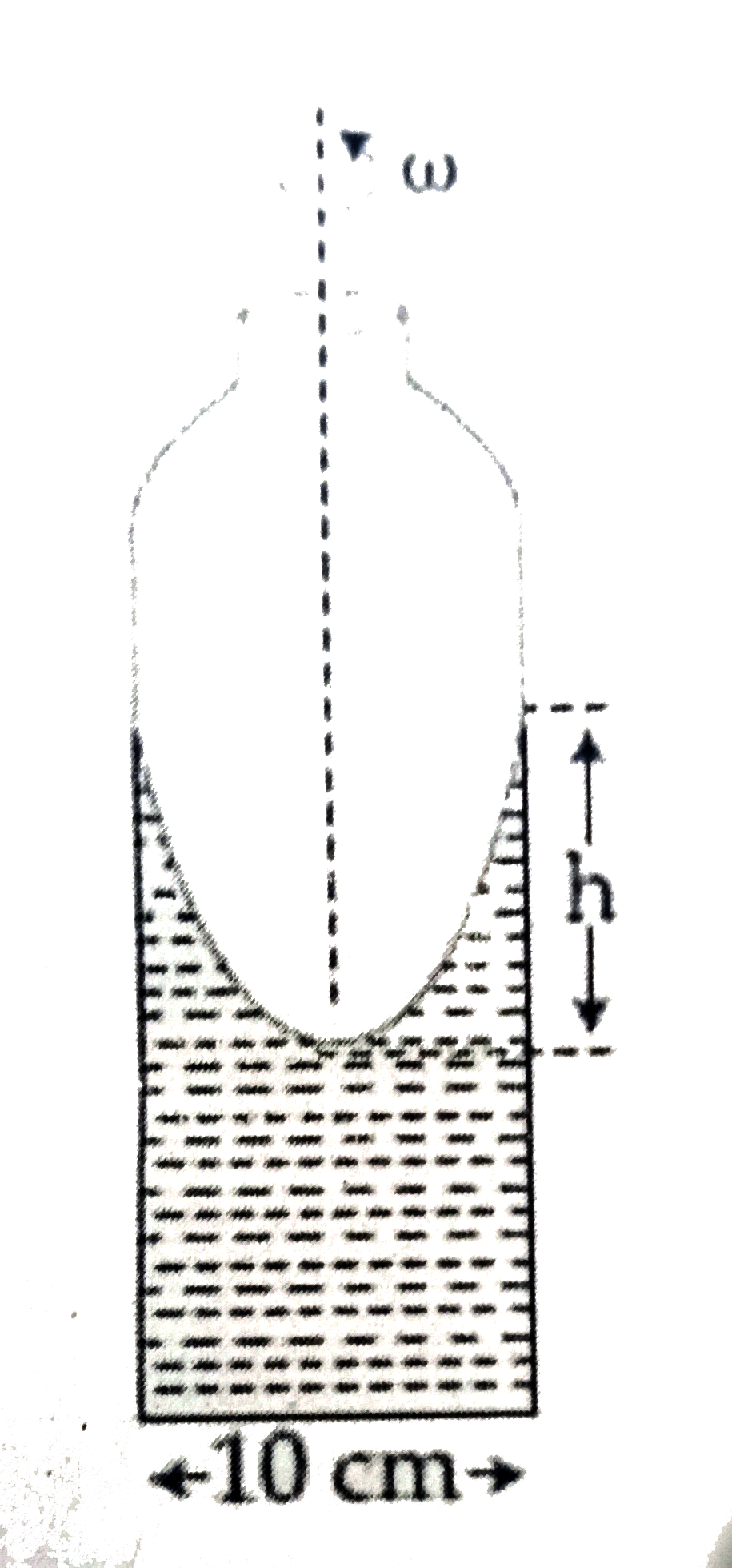
View SolutionA long cylindrical vessel is half filled with a liquid. When the vessel is rotated about its own vertical axis, the liquid rises up near the wall. If the radius of vessel is 5 cm and its rotational speed is 2 rotations per second, then the difference in the heights between the centre and the sides, in cm, will be:
View SolutionA cylindrical vessel of radius r containing a liqiud is rotating about a vertical axis through the centre of circular base, If the vessel is rotating with angular velocity ω then what is the difference of the heights of liquid at centre of vessel and edge?
View SolutionA cylinder vessel of radius 10 cm containing a liquid is rotating about a vertical axis through the centre of circular base. The vessel is rotating with angular frequency 10 rad/s. Find the difference of the heights of liquid at centre of vessel and edge.
View SolutionA conical vessel wihout a bottom stands on a table. A liquid is poured with the vessel & as soon as the level reaches h, the pressure of the liquid raises the vessel. The radius of the base of the vessel is R and half angle of the cone α and the weight of the vessel is W. What is the density of the liquid ?

View SolutionTo what height h should a cylindrical vessel of diameter d be filled with a liquid so that the total force on the vertical surface of the vessel be equal to the force on the bottom-
View SolutionThe bottom of a cylindrical vessel has a circlular hole of radius r and at depth h below the water] level. If the diameter of the vessel is D, the find then speed with which the water level in the] vessel drops.
View Solution