A metallic wire having length of 2 m and weight of 4×10−3 N is found to remain at rest in a uniform and transverse magnetic field of 2×10−4T. Current flowing through the wire is :
10A
5A
2A
1A
The correct Answer is:4A
To solve the problem, we need to find the current flowing through a metallic wire that remains at rest in a uniform and transverse magnetic field. Here's the step-by-step solution:
Step 1: Understand the Forces Acting on the Wire
Since the wire is at rest, the net force acting on it must be zero. This means that the weight of the wire (W) is balanced by the magnetic force (F) acting on it.
Step 2: Write the Equation for Forces
The weight of the wire (W) can be expressed as:
W=m⋅g
where m is the mass of the wire and g is the acceleration due to gravity. However, we are given the weight directly:
W=4×10−3N
The magnetic force (F) on the wire in a magnetic field can be expressed as:
F=B⋅I⋅L
where:
- B is the magnetic field strength,
- I is the current flowing through the wire,
- L is the length of the wire.
Step 3: Set the Forces Equal
Since the wire is at rest, we can set the weight equal to the magnetic force:
W=F
4×10−3N=B⋅I⋅L
Step 4: Substitute Known Values
We know:
- B=2×10−4T
- L=2m
Substituting these values into the equation:
4×10−3=(2×10−4)⋅I⋅2
Step 5: Simplify the Equation
Now, simplify the equation:
4×10−3=4×10−4⋅I
Step 6: Solve for Current (I)
To find I, divide both sides by 4×10−4:
I=4×10−34×10−4
I=10A
Final Answer
The current flowing through the wire is:
I=10A
Since the wire is at rest, the net force acting on it must be zero. This means that the weight of the wire (W) is balanced by the magnetic force (F) acting on it.
The weight of the wire (W) can be expressed as:
W=m⋅g
where m is the mass of the wire and g is the acceleration due to gravity. However, we are given the weight directly:
W=4×10−3N
F=B⋅I⋅L
where:
- B is the magnetic field strength,
- I is the current flowing through the wire,
- L is the length of the wire.
Since the wire is at rest, we can set the weight equal to the magnetic force:
W=F
4×10−3N=B⋅I⋅L
We know:
- B=2×10−4T
- L=2m
4×10−3=(2×10−4)⋅I⋅2
Now, simplify the equation:
4×10−3=4×10−4⋅I
To find I, divide both sides by 4×10−4:
I=4×10−34×10−4
I=10A
The current flowing through the wire is:
I=10A
Similar Questions
A charged oil drop weighing 1.6×10−15N is found to remain suspended in a uniform electric field of intensity 2×103NC−1. Find the charge on the drop.
View SolutionA rectangular coil having 60 turns and area of 0.4 m2 is held at right angles to a uniform magnetic field of flux density 5×10−5T. Calculate the magnetic flux passing through it.
View Solution
Knowledge Check
A tightly wound 90 turn coil of radius 15 cm has a magnetic field of 4×10−4T at its centre. The current flowing through it is
A1.06AB2.44AC3.44AD4.44AA 2.5 m long straight wire having mass of 500 g is suspended in mid air by a uniform horizontal magnetic field B. If a current of 4 A is passing through the wire then the magnitude of the field is (Take g 10ms−2)
A0.5TB0.6TC0.25TD0.8TThe magnetic force per unit length on a wire carrying a current of 10 A and making an angle of 45∘ with the direction of a uniform magnetic field of 0.20 T is
A2√2Nm−1B2√2Nm−1C√22Nm−1D4√2Nm−1
A wire made of aluminum having resistivity ρ=2.8×10−8Ω−m with a circular cross - section and has a radius of 2×10−3 m. A current of 5 A flows through the wire . If the voltage difference between the ends is 1 V , the length of the wire in m is
View SolutionA steel wire has a length of 12 m and mass of 2.10 kg . What will be the speed of a transverse wave on this when a tension of 2.06×104N is applied?
View SolutionA triangular system of mass 100 gm consisting of 3 wires of length, as shown in Fig and length of AO as 4 units, are placed in the magnetic field of 1T. The current of 1 A flows through wire AO. The wires are of same material and cross-sectional area. In which direction will the system move?
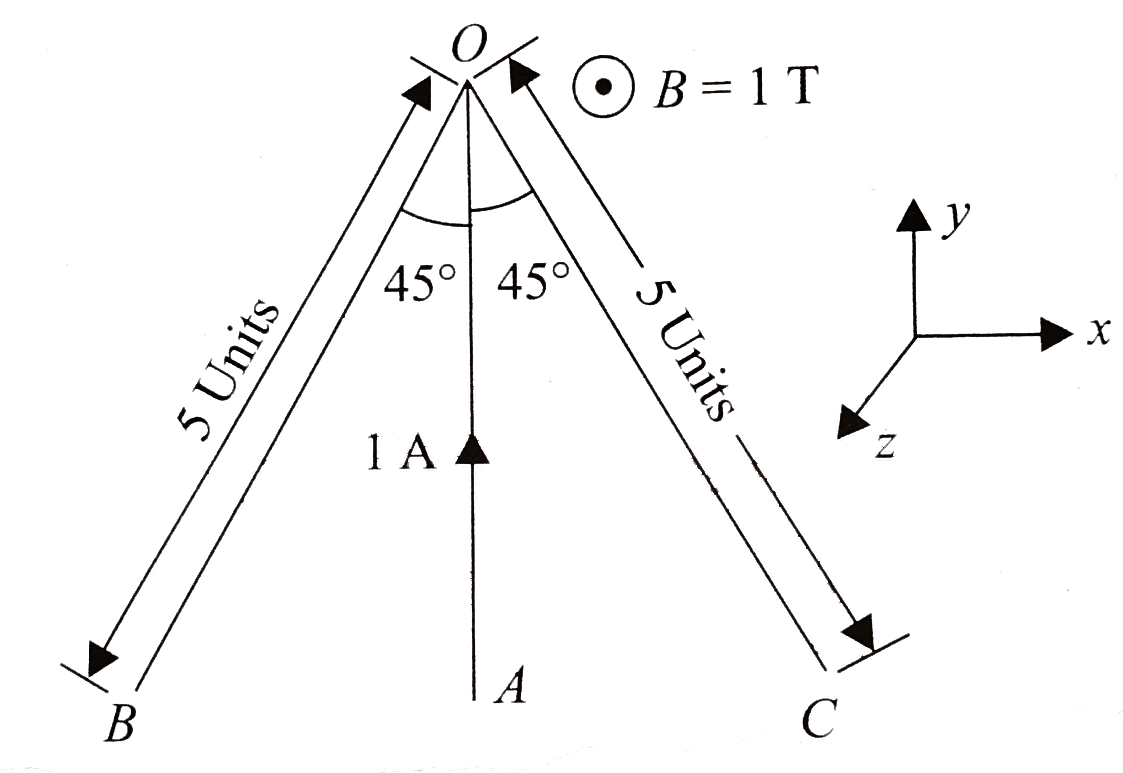
View SolutionA bar magnet having a magnetic moment of 2×104JT−1 is free to rotate in a horizontal plane. A horizontal magnetic field B=6×10−4T exists in the space. The work done in taking the magnet slowly from a direction parallel to the field to a direction 60∘ from the field is
View SolutionA long straight wire carrying current of 30A is placed in an external uniform magnetic field of induction 4×10−4T. The magnetic field is acting parallel to the direction of current. The magnitude of the resultant magnetic induction in tesla at a point 2.0cm away from the wire is
View Solution
