A charged oil drop weighing 1.6×10−15N is found to remain suspended in a uniform electric field of intensity 2×103NC−1. Find the charge on the drop.
To solve the problem of finding the charge on a suspended oil drop, we can follow these steps:
1. Understand the Forces Acting on the Oil Drop:
- The oil drop is suspended in an electric field, which means the electric force acting on it is equal to the gravitational force (weight) acting on it.
- The weight of the oil drop is given as W=1.6×10−15N.
- The intensity of the electric field is given as E=2×103N/C.
2. Set Up the Equation:
- The electric force Fe acting on the charged oil drop can be expressed as:
Fe=Q⋅E
- Since the drop is suspended, the electric force equals the weight:
Q⋅E=W
3. Rearrange the Equation to Solve for Charge Q:
- We can rearrange the equation to find the charge Q:
Q=WE
4. Substitute the Known Values:
- Substitute the values of W and E into the equation:
Q=1.6×10−15N2×103N/C
5. Calculate the Charge:
- Performing the calculation:
Q=1.6×10−152×103=0.8×10−18C
- This can also be expressed in a more standard form:
Q=8×10−19C
Final Answer:
The charge on the oil drop is Q=8×10−19C.
- The oil drop is suspended in an electric field, which means the electric force acting on it is equal to the gravitational force (weight) acting on it.
- The weight of the oil drop is given as W=1.6×10−15N.
- The intensity of the electric field is given as E=2×103N/C.
- The electric force Fe acting on the charged oil drop can be expressed as:
Fe=Q⋅E
- Since the drop is suspended, the electric force equals the weight:
Q⋅E=W
- We can rearrange the equation to find the charge Q:
Q=WE
- Substitute the values of W and E into the equation:
Q=1.6×10−15N2×103N/C
- Performing the calculation:
Q=1.6×10−152×103=0.8×10−18C
- This can also be expressed in a more standard form:
Q=8×10−19C
The charge on the oil drop is Q=8×10−19C.
Similar Questions
Two point charges of 3.2×10−19Cand−3.2×10−19C are separated from each other by 2.4×10−10m. The dipole is situated in a uniform electric field of intensity 4×105Vm−1. Calculate the work done in roating the dipole by 180∘.
View SolutionA point charge of 5×10−6C experiences a force of 2×10−3N when kept in a uniform electric field of intensity E. Find E.
View Solution
Knowledge Check
A metallic wire having length of 2 m and weight of 4×10−3 N is found to remain at rest in a uniform and transverse magnetic field of 2×10−4T. Current flowing through the wire is :
A10AB5AC2AD1AA particle of mass 10−3kg and charge 5μC is thrown at a speed of 20ms−1 against a uniform electric field of strength 2×105NC−1. The distance travelled by particle before coming to rest is
A0.1 mB0.2 mC0.3 mD0.4 m
A charged particle of mass 5×10−5kg is held stationary in space by placing it in an electric field of strength 107NC−1 directed vertically downwards. The charge on the particle is
View SolutionA charged particle of radius 5×10−7m is located in a horizontal electric field of intensity 6.28×105Vm−1. The surrounding medium has the coeffecient of viscosity η=1.6×10−5Nsm−2. The particle starts moving under the effect of electric field and finally attains a uniform horizontal speed of 0.02ms−1. Find the number of electrons on it. Assume gravity free space.
View SolutionIn 1909, Robert Millikan war the firest to find the charge of an electron in his now-famous oil-drop experiment. In that experiment, tiny oil drops were sprayed into a uniform electric field between a horizontal pair of opposite charged plates. The drops were pbserved with a magnitue eyepiece, and the electric field was adjusted so that upward force on some negatively charged oil drops was just sufficient to balance the downward force of gravity. That is, when suspended, upward force qE just equaled mg. Millikan accurately measured the charges on many oil drops and found the values to be whole number multiples of 1.6×10−19C− the charge of the electron. For this, he won the Nobel prize.
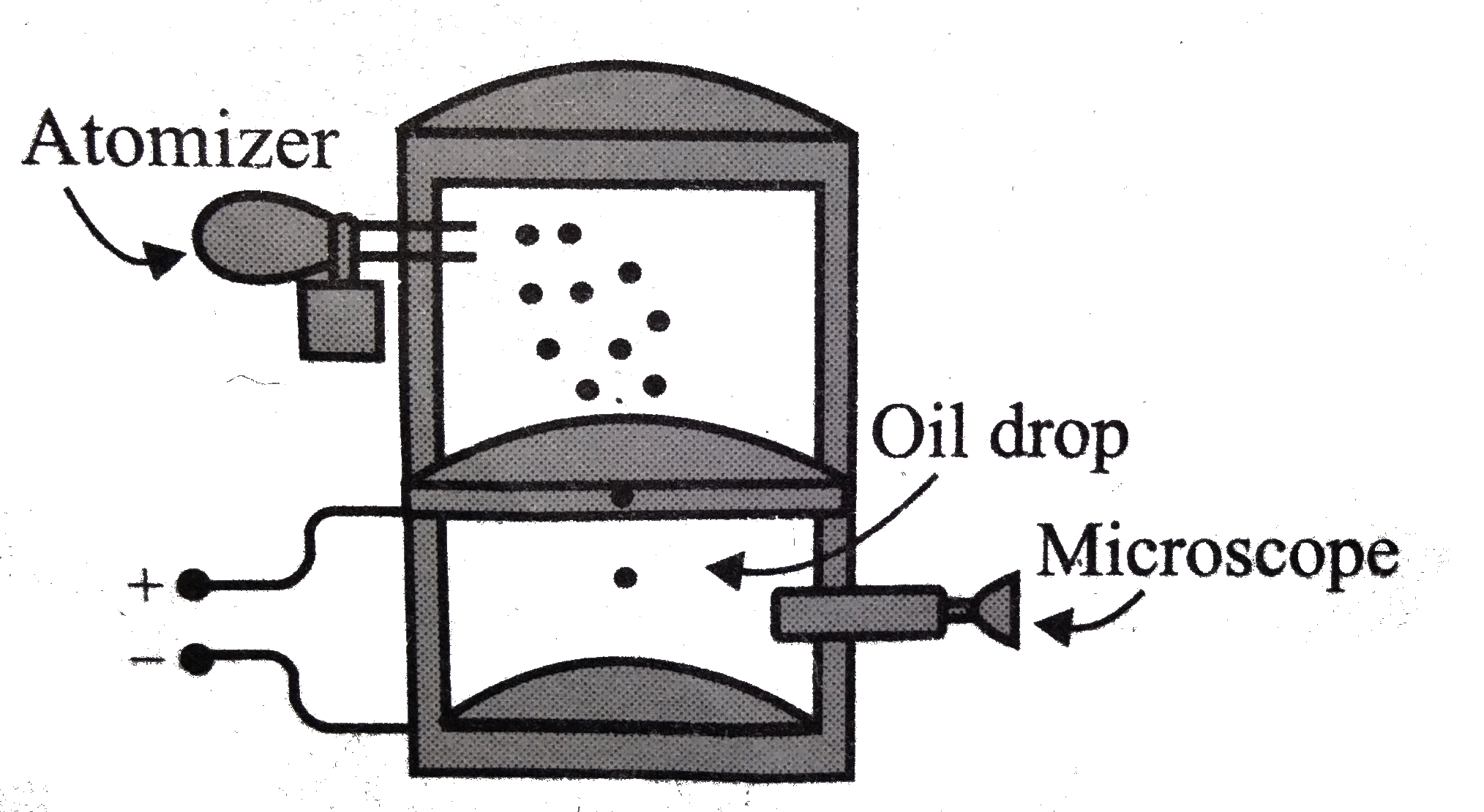
If a drop of mass 1.08×10−14kg remains stationary in an electric field of 1.68×105NC−1, then teh charge of this drop is
View SolutionA charged dust particle of radius 5×10−7m is located in a horizontal electric field having an intensity of 6.28×105Vm−1. The surrounding medium in air with coefficient of viscosity η=1.6×10−15Nsm−2 . If this particle moves with a uniform horizontal speed of 0.01ms−1, the number of electrons on it will be
View SolutionA 0.50 gm ball carries a charge of magnitude 10μC. It is suspended by a string in a downward electric field of intensity 300N/C. If the charge on the ball is positive, then the tension in the string is (g=10ms−2)
View SolutionTwo charges +3.2×10−19Cand−3.2×10−19C placed at 2.4A∘ apart form an electric dipole. It is placed in a uniform electric field of intensity 4×105 volt/m. The electric dipole- moment is
View Solution
