Find magnetic flux density at a point on the axis of a long solenoid having 5000 turns/m when it carrying a current of 2 A
To find the magnetic flux density (B) at a point on the axis of a long solenoid, we can use the formula:
B=μ0⋅n⋅I
where:
- B is the magnetic flux density,
- μ0 is the permeability of free space (4π×10−7T m/A),
- n is the number of turns per unit length of the solenoid (in turns/m),
- I is the current flowing through the solenoid (in A).
1. Identify the given values:
- Number of turns per meter, n=5000turns/m
- Current, I=2A
2. Use the value of μ0:
- The permeability of free space, μ0=4π×10−7T m/A
3. Substitute the values into the formula:
B=μ0⋅n⋅I
B=(4π×10−7)⋅(5000)⋅(2)
4. Calculate the value:
- First, calculate 4π:
4π≈12.5664
- Now substitute:
B=12.5664×10−7⋅5000⋅2
- Calculate 5000⋅2=10000:
B=12.5664×10−7⋅10000
- Now calculate:
B=12.5664×10−3T=0.0125664T
5. Final Result:
- Rounding to four significant figures, we find:
B≈0.0126T
Final Answer:
The magnetic flux density at a point on the axis of the solenoid is approximately 0.0126T.
- B is the magnetic flux density,
- μ0 is the permeability of free space (4π×10−7T m/A),
- n is the number of turns per unit length of the solenoid (in turns/m),
- I is the current flowing through the solenoid (in A).
- Number of turns per meter, n=5000turns/m
- Current, I=2A
- The permeability of free space, μ0=4π×10−7T m/A
B=μ0⋅n⋅I
B=(4π×10−7)⋅(5000)⋅(2)
- First, calculate 4π:
4π≈12.5664
- Now substitute:
B=12.5664×10−7⋅5000⋅2
- Calculate 5000⋅2=10000:
B=12.5664×10−7⋅10000
- Now calculate:
B=12.5664×10−3T=0.0125664T
- Rounding to four significant figures, we find:
B≈0.0126T
The magnetic flux density at a point on the axis of the solenoid is approximately 0.0126T.
Similar Questions
Knowledge Check
- Question 1 - Select One
The torque required to hold a small circular coil of 10 turns, area 1mm2 and carrying a current of (2144)A in the middle of a long solenoid of 103turns/m carrying a current of 2.5A, with its axis perpendicular to the axis of the solenoid is
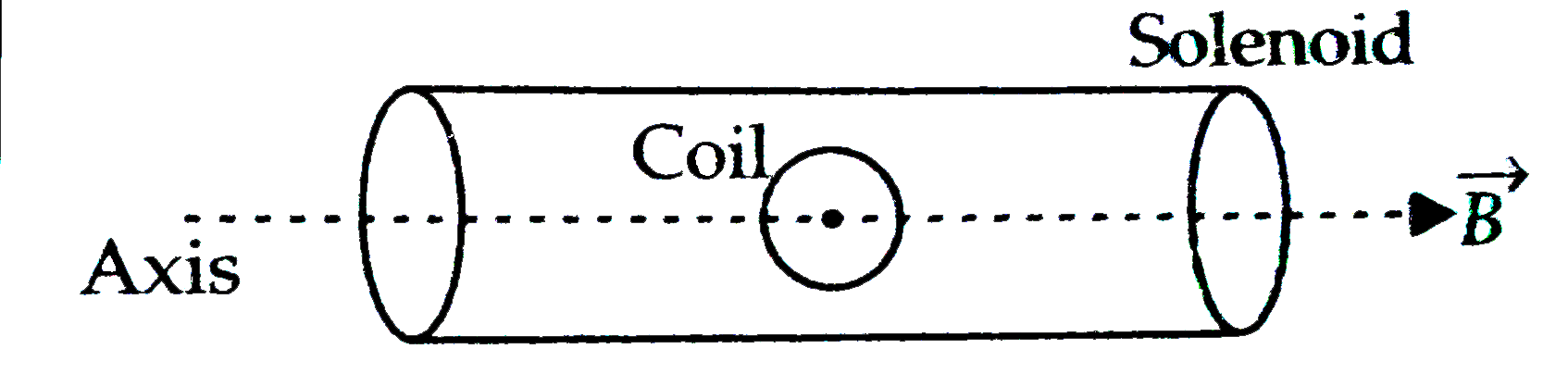 A1.5×10−6NmB1.5×10−8NmC1.5×106NmD1.5×108Nm
A1.5×10−6NmB1.5×10−8NmC1.5×106NmD1.5×108Nm
Find the magnetic intensity H at the centre of a long solenoid having n turns per unit length and carrying a current i (a) when no material is kept in it and (b) when a long copper rod is inserted in the solenoid.
View SolutionObtain an expression for magnetic flux density B at the centre of a circular coil of radius R, having N turns and carrying a current I.
View SolutionObtain an expression for magnetic flux density B at the centre of a circular coil of radius R, having N turns and carrying a current I.
View SolutionThe magnetic flux density at a point distant d from a long straight current carrying conductor is B, then its value at distance d2 will be-
View SolutionA bar magnet is demagnetized by inserting it inside a solenoid of length 0.2 m, 100 turns, and carrying a current of 5.2 A. The coercivity of the bar magnet is :
View SolutionA bar magnet is demagnetized by inserting it inside a solenoid of length 0.2 m, 100 turns, and carrying a current of 5.2 A. The coercivity of the bar magnet is :
View SolutionFind the magnetic field induction at a point on the axis of a circular coil carrying current and hence find the magnetic field at the centre of circular coil carrying current.
View Solution


