Obtain an expression for magnetic flux density B at the centre of a circular coil of radius R, having N turns and carrying a current I.
Magnetic field at O due to small element δl.
δB=μ04πIδlsinθR2
But θ=90∘
∴δB=μ04πIδlR2
→B at O due to the whole circular coil is given by
B∫dB=∫μ04πidlR2
=μ04πiR2⋅2πR=μ0i2
If there are N turns in the coil, then
B=μ0Ni2R
Alternate method : Consider a circular loop of wire of radius .a. carrying current i. Let P be a point on the axis of the coil, at a distance x from its centre O
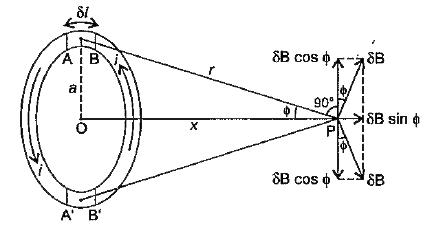
The resultant magnetic field at P is given by
B=∫dBsinϕ
But sinϕ=ar
B=∫μ04πir2×ardl
=∫μ04πiar3dl
Now, since the terms μ0/4π. i and a are constants and r has the same value for all the elements of loop. Thus, the term μ0ia/4πr3 can be factored out of integration.
∴B=μ04π=iar3∫dl
But ∫dl=2πa (circumference of the loop) and r=(a2+x2)1/2.
∴B=μ04π2πia2(a2+x2)3/2
=μ0ia22(a2+x2)3/2
It is a coil of N turns, then each turn will contribute equally to B. Thus,
B=μ0Nia22(a2+x2)3/2
The direction of magnetic field →B is along the axis of the loop and of the coil.
At the centre of the coil,
∴B=μ0Nia22(a2+0)3/2=μ0Ni2a
Similar Questions
(a) Using Biot-Savart's law, derive an expression for the magnetic field at the centre of a circular coil of radius R, number of turns N, carrying current.
(b) Two small identical circular coils marked 1,2 carry equal currents and are placed with their geometric axes perpendicular to each other as shown in the figure. Derive an expression for the resultant magnetic field at O.

View SolutionCalculate magnetic flux density of the magnetic field at the centre of a circular coil of 50 turns, having radius of 0.5 m and carrying a current of 5A.
View Solution
Knowledge Check
The magnetic moment of a current I carrying circular coil of radius r and number of turns N varies as
A1r2B1rCrDr2
Find magnetic flux density at a point on the axis of a long solenoid having 5000 turns/m when it carrying a current of 2 A
View Solution(a) Write the expression for the equivalent megnetic moment of a planer current loop of area A, having N turns and carrying a current i. Use the expression to find the magentic dipole moment of a revolving electron ?
(b) A circuit loop of radius r, having N turns and carrying current I, is kept in the XY plane. It is then subjected to a uniform magnetic field →B=Bxˆi+Byˆj+Bzˆk . Obtain expression for the magnetic potential energy of the coil-magnetic field system.
View SolutionMagnetic field intensity at the centre of coil of 50 turns, radius 0.5m and carrying a current of 2A is
View SolutionThe magnetic field at the centre of the current carrying coil is
View SolutionThe magneitc field produced at the center of a current carrying circular coil of radius r, is
View Solution(a) State Biot - Savart law and ecpress it in the vector form.
(b) Using Biot - Savart law, law obtain the expression for the magnetic field due to a circular coil of radius r, carrying a current I at point on its axis distant x from the centre of the coil.
View SolutionUsing Ampere.s circuital law, obtain an expression for the magnetic flux density .B. at a point .X. at a perpendicular distance .r. from a long current carrying conductor. (Statement of the law is not required).
View Solution
