A fish which is at a depth of 12 cm in water (μ=43) is viewed by an observer on the bank of a lake. Its apparent depth as observed by the observer is :
3 cm
9 cm
12 cm
16 cm
The correct Answer is:B
To find the apparent depth of the fish as observed by the observer on the bank of the lake, we can use the formula that relates the real depth, apparent depth, and the refractive index of the medium:
μ=Real DepthApparent Depth
Where:
- μ is the refractive index of water,
- Real Depth is the actual depth of the fish,
- Apparent Depth is the depth at which the fish appears to be located when viewed from above the water.
1. Identify the given values:
- Real Depth (d) = 12 cm
- Refractive Index (μ) = 43
2. Use the formula for refractive index:
μ=Real DepthApparent Depth
Substituting the known values:
43=12 cmApparent Depth
3. Rearranging the formula to find Apparent Depth:
Apparent Depth=Real Depthμ
Substituting the values:
Apparent Depth=12 cm43
4. Calculating Apparent Depth:
- To divide by a fraction, multiply by its reciprocal:
Apparent Depth=12 cm×34
Apparent Depth=36 cm4=9 cm
5. Conclusion:
The apparent depth of the fish as observed by the observer is 9 cm.
Final Answer:
The apparent depth of the fish is 9 cm.
---
- μ is the refractive index of water,
- Real Depth is the actual depth of the fish,
- Apparent Depth is the depth at which the fish appears to be located when viewed from above the water.
- Real Depth (d) = 12 cm
- Refractive Index (μ) = 43
μ=Real DepthApparent Depth
Substituting the known values:
43=12 cmApparent Depth
Apparent Depth=Real Depthμ
Substituting the values:
Apparent Depth=12 cm43
- To divide by a fraction, multiply by its reciprocal:
Apparent Depth=12 cm×34
Apparent Depth=36 cm4=9 cm
The apparent depth of the fish as observed by the observer is 9 cm.
The apparent depth of the fish is 9 cm.
Similar Questions
A diver at a depth of 12 m in water (μ=4/3) sees the sky in a cone of semi-vertical angle
View SolutionAn object lies 100 cm inside water (μ=4/3). It is viewed from air nearly normally. Find the apparent depth of the object.
View Solution(a) In the figure shown a slab of refractive index 32 is moved toward a stationary observer with speed 6cm/s . A point O is observed by the observer with the help of paraxial rays through the slab. Both O and observer lie in are. Find the velocity (in cm/s) with which the image will appear to move to observer.
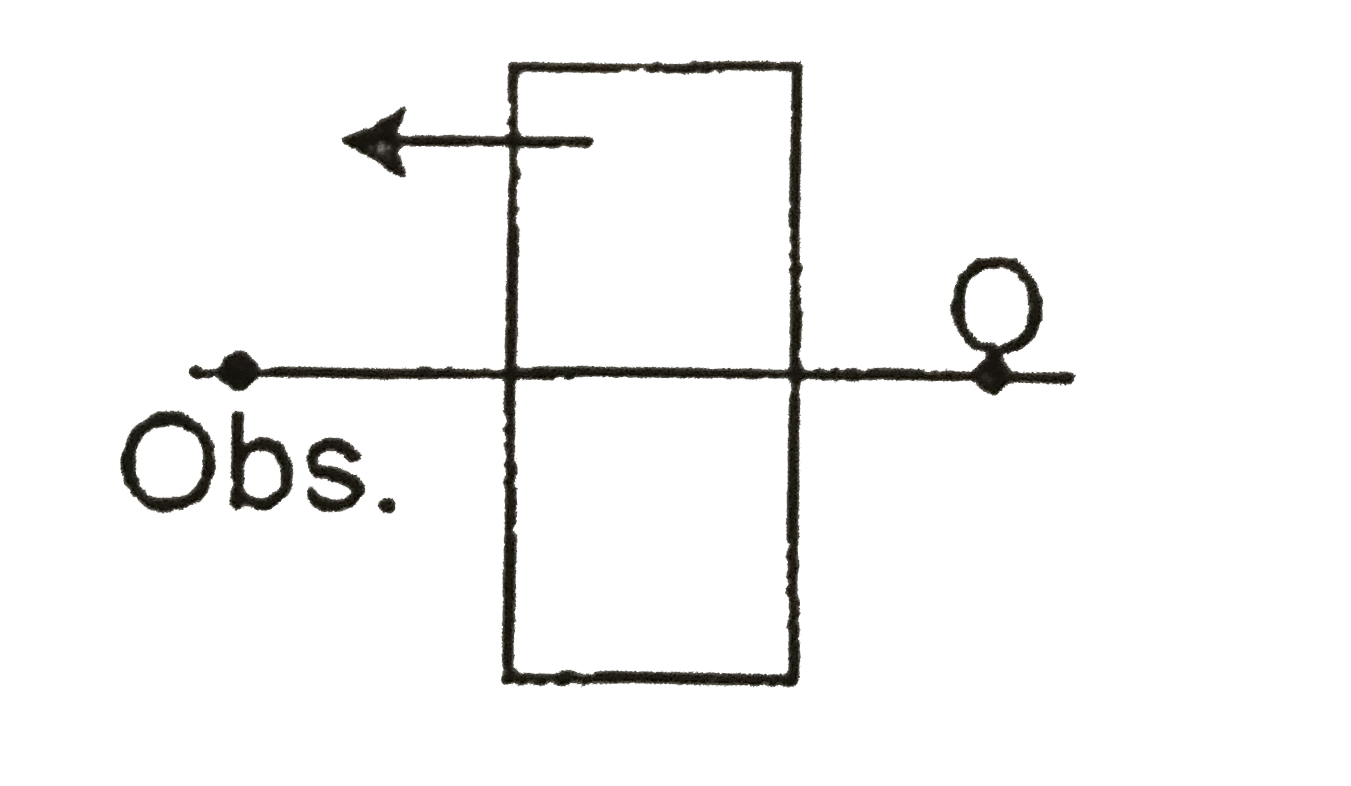
(b) in the previous question if the object moves towards rigth with a velocity of 6cm/s and find the velocity of the final image (in cm/s) as seen by observer :View SolutionFind the apparent depth of object of the object seen by observe A (in the figure shown)
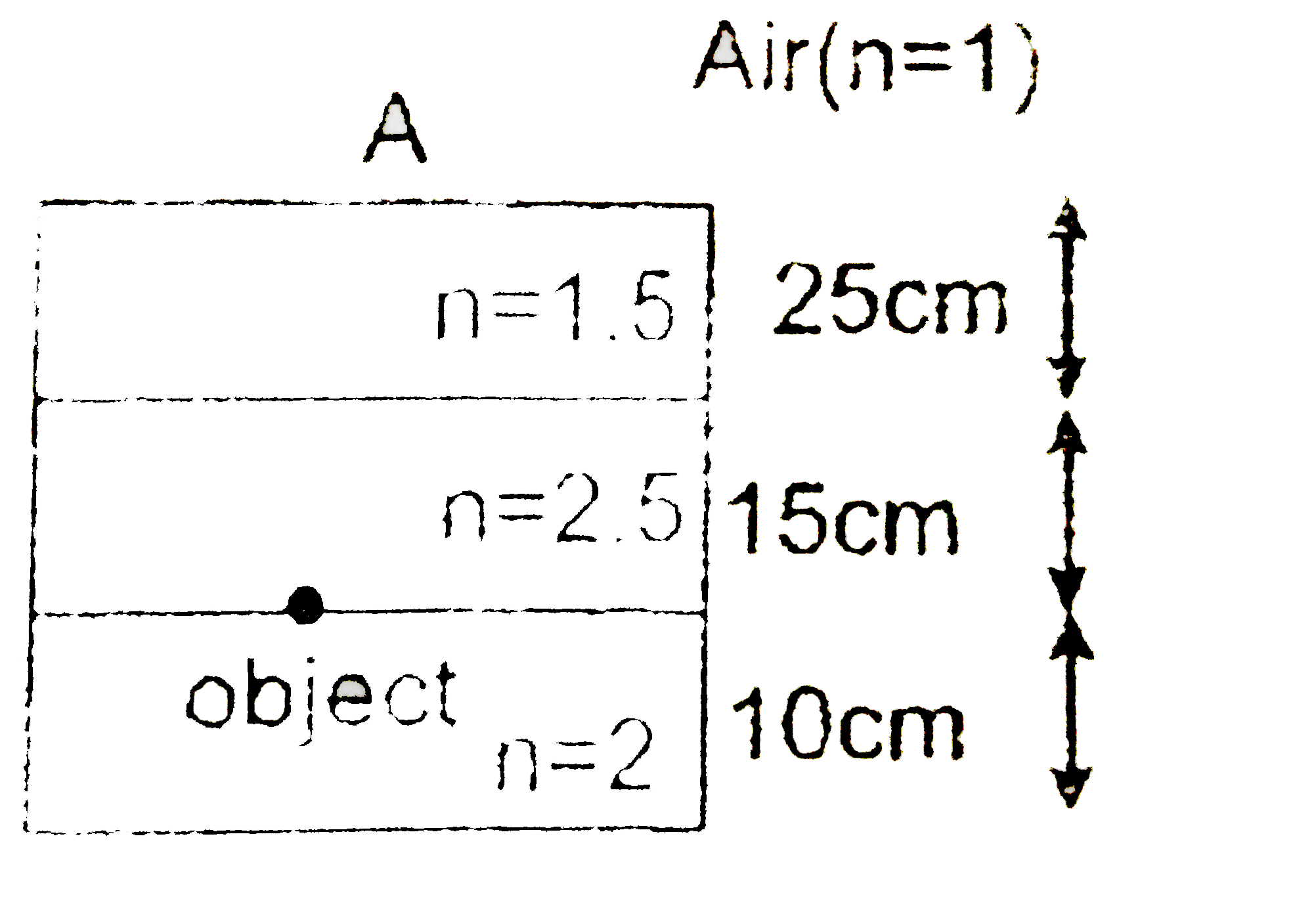 View Solution
View SolutionFind the apparent depth of object O below surface AB, seen by an observer in mediumn of refractive index μ2
 View Solution
View SolutionA block of mass m1 moves with an acceleration a12 relative to a trolley as shown in figure. The block is being observed by two observers (2) and (3). The observer (2) is at rest with respect to trolley which is moving with acceleration a2 while the observer(3) is moving on ground with acceleration a3. What is the work done by the pseudo force as observed by the observers (2) and (3) on the block during time t? Assume zero intial velocities of the bodies and observers.
 View Solution
View SolutionThe lower end of a capillary tube is at a depth of 12cm and water rises 3cm in it. The mouth pressure required to blow an air bubble at the lower end will be xcm of water column, where x is
View SolutionIn above question if observer is in medium μ3 what is the apparenet depth of object seen below surface 1CD.
View SolutionStatement I: The apparent freqeuncy which is the frequency as noted by an observer or an observing detection device of the acoustic wave that moves from the source to the observer propagating in a medium may be different from its true frequency.
Statement II: A source in motion relative to an observer sends out less or more number of waves per metre distance in the medium and an observer in motion collects less or more number of waves per second that when both of them remain at rest relatively.View SolutionA small fish 0.4 m below the surface of a lake is viewed through a simple converging lens of focal length 3 m.the lens is kep at 0.2 m above the water surface such that the fish lies on the optical axis of the lens. Find the image of the fish seen by the observed. (μwater=43)
View Solution

