In above question if observer is in medium μ3 what is the apparenet depth of object seen below surface 1CD.
To find the apparent depth of an object seen below the surface CD when the observer is in medium with refractive index μ3, we can follow these steps:
1. Identify the Mediums and Their Refractive Indices:
- Let the refractive index of the medium above surface CD be μ1.
- The refractive index of the medium below surface CD (where the object is located) is μ2.
- The refractive index of the medium where the observer is located is μ3.
2. Determine the Thicknesses:
- Let t1 be the thickness of the medium with refractive index μ1 above the object.
- Let t2 be the thickness of the medium with refractive index μ2 below the object.
3. Calculate the Apparent Depth:
- The apparent depth dA can be calculated using the formula:
dA=t1μ1,3+t2μ2,3
- Here, μ1,3 is the relative refractive index of the medium above the object with respect to the observer, which is given by:
μ1,3=μ1μ3
- Similarly, μ2,3 is the relative refractive index of the medium below the object with respect to the observer:
μ2,3=μ2μ3
4. Substituting the Values:
- Substitute μ1,3 and μ2,3 into the formula for dA:
dA=t1⋅μ3μ1+t2⋅μ3μ2
5. Final Expression:
- Therefore, the total apparent depth dA is given by:
dA=μ3(t1μ1+t2μ2)
- Let the refractive index of the medium above surface CD be μ1.
- The refractive index of the medium below surface CD (where the object is located) is μ2.
- The refractive index of the medium where the observer is located is μ3.
- Let t1 be the thickness of the medium with refractive index μ1 above the object.
- Let t2 be the thickness of the medium with refractive index μ2 below the object.
- The apparent depth dA can be calculated using the formula:
dA=t1μ1,3+t2μ2,3
- Here, μ1,3 is the relative refractive index of the medium above the object with respect to the observer, which is given by:
μ1,3=μ1μ3
- Similarly, μ2,3 is the relative refractive index of the medium below the object with respect to the observer:
μ2,3=μ2μ3
- Substitute μ1,3 and μ2,3 into the formula for dA:
dA=t1⋅μ3μ1+t2⋅μ3μ2
- Therefore, the total apparent depth dA is given by:
dA=μ3(t1μ1+t2μ2)
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Exercise-1141videos
GEOMATRICAL OPTICS
- BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Exercise-262videos
GEOMATRICAL OPTICS
- BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Advance level Problems35videos
GEOMATRICAL OPTICS
- BOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II10videos
EXPERIMENTAL PHYSICS
- BOOK - RESONANCE ENGLISHCHAPTER - GRAVITATIONEXERCISE - HIGH LEVEL PROBLEMS16videos
GRAVITATION
Similar Questions
In Fig. , find the apparent depth of the object seen below surface AB.
 View Solution
View SolutionA glass sphere of (μ=1.5) with a radius of 15.0cm has a tiny air bubble 5cm above its centre. The sphere is viewed looking down along the extended radius containing the bubble. What is the apparent depth of the bubble below the surface of the sphere?
View Solution
Knowledge Check
- Question 1 - Select One
A vesse of depth x is half filled with oil of refractive index μ1 and the other half is filled with water of refrative index μ2. The apparent depth of the vessel when viewed above is
Ax(μ1+μ2)2μ1μ2Bxμ1μ22(μ1+μ2)Cxμ1μ2(μ1+μ2)D2x(μ1+μ2)μ1μ2
Using formula of spherical surface or otherwise, find the apparent depth of an object placed 10cm below the water surface, if seen near normally form air.
View SolutionA layer of benzene (μ=1.5) 12 cm thick floats on water layer (μ=4/3) 8 cm thick in a vessel. When viewed from the top, the apparent depth of bottom of vessel below the surface of benzene will be
View SolutionA glass sphere (μ=1.5) of radius 20 cm has a small air bubble 4 cm below its centre. The sphere is viewed from outside and along a vertical line through the bubble. The apparent depth of the bubble below the surface of sphere is (in cm)
View SolutionA man observes a coin placed at the bottom of a beaker which contains two immiscible liquids of refractive indices 1.2 and 1.4 as shown in the figure. Find the depth of the coin below the surface, as observed from above.
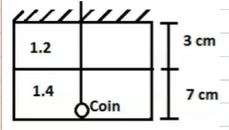 View Solution
View SolutionFind the apparent depth of object of the object seen by observe A (in the figure shown)
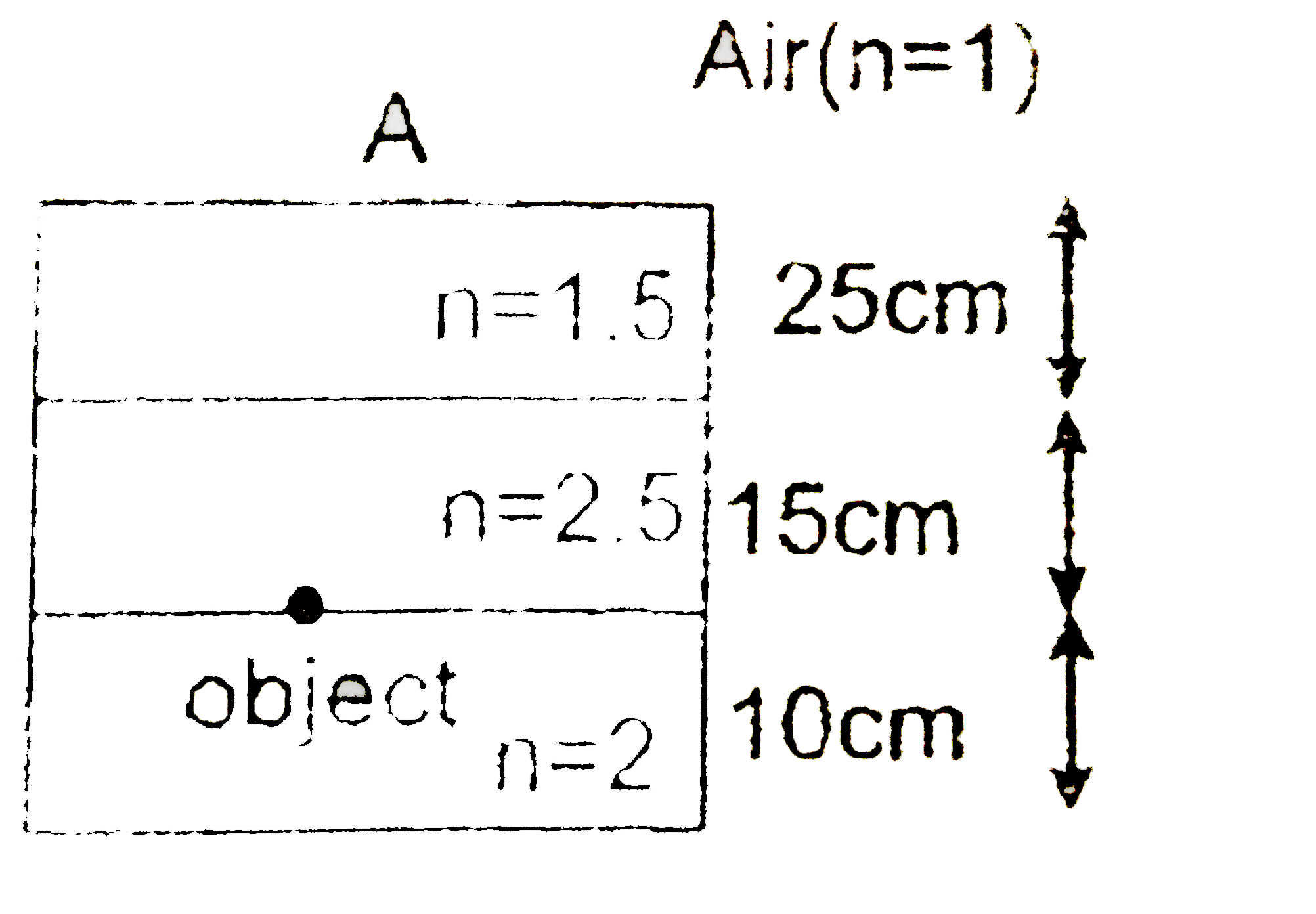 View Solution
View SolutionA cylinder is filled with a liquid of refractive index μ. The radius of the cylinder is decreasing at a constant rate K. The volume of the liquid inside the container remains constant at V. The observer and the object O are in a state of rest at a distance L from each other. When radius of cylinder is r the apparent velocity of the object as seen by the observer is
 View Solution
View SolutionThe acceleration due to gravity at a height 1km above the earth is the same as at a depth d below the surface of earth. Then :
View Solution

