Two resistors are connected in parallel to a battery. If heating power developed in is 25. W. find the heating power developed in .
To solve the problem step by step, we will use the relationship between power, resistance, and voltage in a parallel circuit.
Step 1: Understand the given values
We have two resistors:
- R1=400Ω
- R2=20Ω
The power developed in resistor R1 is given as:
- P1=25W
We need to find the power developed in resistor R2, which we will denote as P2.
Step 2: Use the formula for power in terms of voltage and resistance
In a parallel circuit, the voltage across both resistors is the same. The power developed in a resistor can be expressed as:
P=V2R
where V is the voltage across the resistor and R is the resistance.
Step 3: Relate the powers and resistances
Since the voltage across both resistors is the same, we can set up the following equation using the power formula:
V2R1=P1andV2R2=P2
From this, we can express V2 in terms of P1 and R1:
V2=P1⋅R1
Substituting this into the equation for P2:
P2=V2R2=P1⋅R1R2
Step 4: Substitute the known values
Now we can substitute the known values into the equation:
P2=25W⋅400Ω20Ω
Step 5: Calculate P2
Now perform the calculation:
P2=1000020=500W
Conclusion
The heating power developed in resistor R2 is:
P2=500W
We have two resistors:
- R1=400Ω
- R2=20Ω
- P1=25W
In a parallel circuit, the voltage across both resistors is the same. The power developed in a resistor can be expressed as:
P=V2R
where V is the voltage across the resistor and R is the resistance.
Since the voltage across both resistors is the same, we can set up the following equation using the power formula:
V2R1=P1andV2R2=P2
From this, we can express V2 in terms of P1 and R1:
V2=P1⋅R1
Substituting this into the equation for P2:
P2=V2R2=P1⋅R1R2
Now we can substitute the known values into the equation:
P2=25W⋅400Ω20Ω
Now perform the calculation:
P2=1000020=500W
The heating power developed in resistor R2 is:
P2=500W
Similar Questions
Knowledge Check
- Question 1 - Select One
Two resistances R1=100±3ΩandR2=200±4Ω are connected in series . Find the equivalent resistance of the series combination.
A(66.7±1.8)ΩB(66.7±4.0)ΩC(66.7±3.0)ΩD(66.7±7.0)Ω
Two resistor R1=(24±0.5)ΩandR2=(8±0.3)Ωare joined in series, The equivalent resistence is
View SolutionTwo resistances R1=100±3ΩandR2=200±4Ω are connected in series . Find the equivalent resistance of the series combination.
View SolutionTwo resistor of resistance R1=(6±0.09)Ω and R2=(3±0.09)Ω are connected in parallel the equivalent resistance R with error (in Ω)
View SolutionTwo resistors of 6Ω and 9Ω are connected in series to a 120 V source. The power consumed by the 6Ω resistor is
View Solution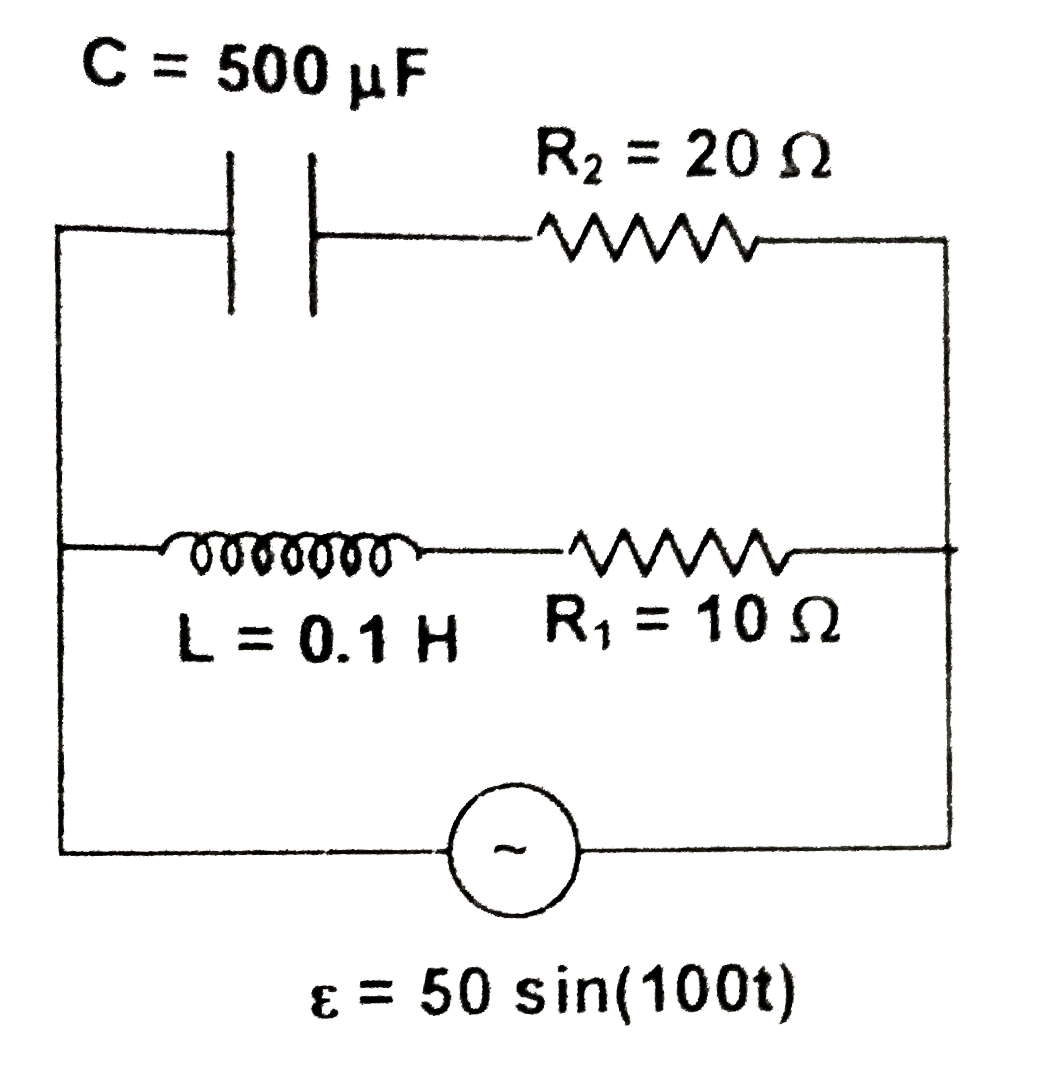
In the circuit shown the average power developed in the resistor R1 isView SolutionThree identical resistors R1=R2=R3 are connected as shown to a battery of constant e.m.f . The power dissipated is
 View Solution
View SolutionTwo resistors of resistance R1=2ΩandR2=1Ω are connected in parallel with a current source of 3 A. Draw the arrangement and deduce the current I1 in R1andI2 in R2.
View Solution