find the minimum wavelength of the emitted X rays, when an X-ray tube is operated at 50 kV.
To find the minimum wavelength of the emitted X-rays when an X-ray tube is operated at 50 kV, we can follow these steps:
1. Identify the given values:
- The operating voltage V=50kV=50×103V.
2. Understand the relationship between energy and wavelength:
- The energy E of the emitted X-rays can be expressed as:
E=eV
where e is the charge of an electron (e=1.6×10−19C).
3. Calculate the maximum energy of the X-rays:
- Substitute the values:
E=eV=(1.6×10−19C)(50×103V)=8.0×10−15J
4. Relate energy to wavelength:
- The energy of a photon is also given by:
E=hcλmin
where h is Planck's constant (h=6.63×10−34Js) and c is the speed of light (c=3×108m/s).
5. Set the two expressions for energy equal to each other:
eV=hcλmin
6. Rearrange to find the minimum wavelength:
λmin=hceV
7. Substitute the known values into the equation:
λmin=(6.63×10−34Js)(3×108m/s)(1.6×10−19C)(50×103V)
8. Calculate the numerator:
hc=6.63×10−34×3×108=1.989×10−25Jm
9. Calculate the denominator:
eV=1.6×10−19×50×103=8.0×10−15J
10. Now calculate λmin:
λmin=1.989×10−258.0×10−15=2.48625×10−11m
or
λmin=0.248625nm=0.248625×10−10m=0.248625Å
11. Final answer:
λmin≈0.25Å
- The operating voltage V=50kV=50×103V.
- The energy E of the emitted X-rays can be expressed as:
E=eV
where e is the charge of an electron (e=1.6×10−19C).
- Substitute the values:
E=eV=(1.6×10−19C)(50×103V)=8.0×10−15J
- The energy of a photon is also given by:
E=hcλmin
where h is Planck's constant (h=6.63×10−34Js) and c is the speed of light (c=3×108m/s).
eV=hcλmin
λmin=hceV
λmin=(6.63×10−34Js)(3×108m/s)(1.6×10−19C)(50×103V)
hc=6.63×10−34×3×108=1.989×10−25Jm
eV=1.6×10−19×50×103=8.0×10−15J
λmin=1.989×10−258.0×10−15=2.48625×10−11m
or
λmin=0.248625nm=0.248625×10−10m=0.248625Å
λmin≈0.25Å
Similar Questions
Find the minimum wavelngth of X - ray emitted by X - ray tube , which is operating at 15kV accelerating voltage.
View SolutionFigure below shows a simple diagram of a modern X ray tube. (i.e. Coolidge tube).
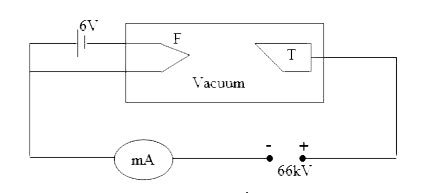
(i) Find the minimum wavelength of the X rays emitted by the X ray tube.
(ii) What will be the effect of replacing the 6V battery with a 9V battery on the emitted X rays?
View SolutionFind the cutoff wavelength for the continuous X-rays coming form an X-ray tube operating at 30 kV.
View SolutionFind the cut off wavelength for the continuous X - rays coming from an X-ray tube operating at 40 kV.
View SolutionFind the maximum frequency, the X-ray emitted by an X-ray tube operating at 30kV
View SolutionFind the maximum frequency, the X-ray emitted by an X-ray tube operating at 30kV
View SolutionFind the cut off walelength for the continuous X - rays coming
form an X-ray tube operating at 40 kv.
View SolutionThe shorted wavelength of X- rays emitted from an X- rays tube depends on
View SolutionThe shorted wavelength of X- rays emitted from an X- rays tube depends on
View SolutionA: If the accelerating potential in an X- ray machine is decreased, the minimum value of the wavelength of the emitted X -rays gets increased.
R: The minimum value of wavelength of the emitted X-rays is inversely proportional to the accelerating potential.
View Solution