A 0.50 gm ball carries a charge of magnitude 10μC. It is suspended by a string in a downward electric field of intensity 300N/C. If the charge on the ball is positive, then the tension in the string is (g=10ms−2)
5×10−3N
8×10−3N
2×10−3N
zero
The correct Answer is:B
To solve the problem, we need to find the tension in the string when a charged ball is suspended in a downward electric field. Let's break it down step by step.
Step 1: Identify the forces acting on the ball
The ball experiences two main forces:
1. Gravitational force (weight) acting downwards.
2. Electric force acting downwards due to the electric field.
Step 2: Calculate the gravitational force (weight)
The weight (W) of the ball can be calculated using the formula:
W=mg
where:
- m=0.50g=0.50×10−3kg
- g=10m/s2
Calculating the weight:
W=0.50×10−3kg×10m/s2=5×10−3N
Step 3: Calculate the electric force
The electric force (F_e) acting on the ball can be calculated using the formula:
Fe=qE
where:
- q=10μC=10×10−6C
- E=300N/C
Calculating the electric force:
Fe=10×10−6C×300N/C=3×10−3N
Step 4: Determine the net force acting on the ball
Since both the gravitational force and the electric force are acting downwards, we can find the total force acting on the ball:
Ftotal=Fe+W
Ftotal=3×10−3N+5×10−3N=8×10−3N
Step 5: Calculate the tension in the string
The tension (T) in the string must balance the total downward force when the ball is in equilibrium. Therefore, the tension in the string is equal to the total downward force:
T=Ftotal=8×10−3N
Final Answer
The tension in the string is 8×10−3N.
---
The ball experiences two main forces:
1. Gravitational force (weight) acting downwards.
2. Electric force acting downwards due to the electric field.
The weight (W) of the ball can be calculated using the formula:
W=mg
where:
- m=0.50g=0.50×10−3kg
- g=10m/s2
W=0.50×10−3kg×10m/s2=5×10−3N
The electric force (F_e) acting on the ball can be calculated using the formula:
Fe=qE
where:
- q=10μC=10×10−6C
- E=300N/C
Fe=10×10−6C×300N/C=3×10−3N
Since both the gravitational force and the electric force are acting downwards, we can find the total force acting on the ball:
Ftotal=Fe+W
Ftotal=3×10−3N+5×10−3N=8×10−3N
The tension (T) in the string must balance the total downward force when the ball is in equilibrium. Therefore, the tension in the string is equal to the total downward force:
T=Ftotal=8×10−3N
The tension in the string is 8×10−3N.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - AAKASH SERIESCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Exercise-II
56 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - AAKASH SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - PRACTICE EXERCISEX
42 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-II)
26 Videos
Similar Questions
A sphere of mass 50gm is suspended by a string in an electric field of intensity 5NC−1 acting vertically upward. If the tension in the string is 520 milli newton, the charge on the sphere is (g=10ms−2)
View SolutionA sphere of mass 50 gm is suspended by a string in an electric field of intensity 5NC−1 acting vertically upward. If the tension in the string is 520 millinewton, the charge on the sphere is (g=10ms−2)
View SolutionA charged oil drop weighing 1.6×10−15N is found to remain suspended in a uniform electric field of intensity 2×103NC−1. Find the charge on the drop.
View SolutionA 10 kg steel ball is suspended by two strings as shown. The tensions in the two strings are: (g=9.8 m/s2)

View SolutionA charged cork of mass m suspended by a light string is placed in uniform electric field filed of strength E=(ˆi+ˆj)×105NC−1 as shown in the figure. If in equilibrium position tension in the string is 2mg/(1+√3) the angle α with the vertical can be
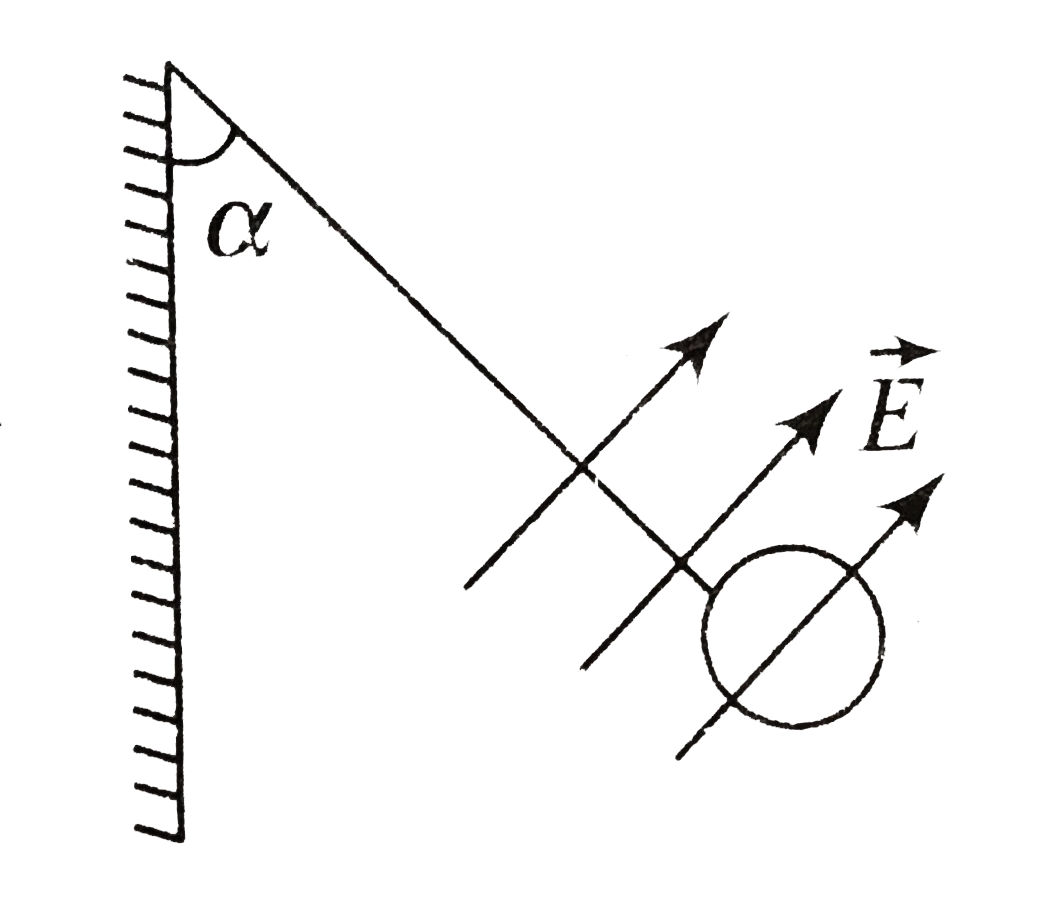
View SolutionTwo charged particles having charge 2.0×10−8C each are joined by an insulating string of length 1 m and the system is kept on a smooth horizontal table. Find the tension in the string.
View SolutionThe electric field due to a point charge at a distance 6 m from it is 630 N/C. The magnitude of the charge is
View SolutionA block of mass 0.2 kg is suspended from the ceiling by a light string. A second block of mass 0.3 kg is suspended from the first block through another string. Find the tensions in the two strings. Take g=10ms2.
View SolutionA charged ball of mass 5.88×10−4 kg is suspended from two silk strings of equal lengths so that the strings are inclined at 60∘ with each other. Another ball carrying a charge which is equal in magnitude but opposite in sign of the first one is placed vertically below the first one at a distance of 4.2×10−2m. Due to this, the tension in the strings is doubled. Determine the charge on the ball and the tension in the strings after electrostatic interaction. (g=9.8m/s2)
View SolutionTwo charged particles having charge 2.0×10−8C. Each are joined by an isolating string of length 1m and the system is kept on a smooth horizontal task. The tension in the string.
View Solution
