For a metallic conductor, what is the relation between current density (J), conductivity (σ) and electric field intensity E?
To derive the relation between current density (J), conductivity (σ), and electric field intensity (E) for a metallic conductor, we can follow these steps:
1. Understanding Conductivity and Resistivity:
- The conductivity (σ) of a material is defined as the reciprocal of its resistivity (ρ). Therefore, we can express this relationship as:
σ=1ρ
2. Defining Resistivity:
- The resistivity (ρ) can be defined in terms of electric field intensity (E) and current density (J). According to the definition, resistivity is given by:
ρ=EJ
- Here, E is the electric field intensity and J is the current density at a point inside the conductor.
3. Substituting Resistivity into Conductivity:
- Now, substituting the expression for resistivity (ρ) into the equation for conductivity (σ):
σ=1ρ=1EJ=JE
4. Rearranging the Equation:
- From the above equation, we can rearrange it to express current density (J) in terms of conductivity (σ) and electric field intensity (E):
J=σ⋅E
Final Relation:
Thus, the relation between current density (J), conductivity (σ), and electric field intensity (E) for a metallic conductor is:
J=σ⋅E
- The conductivity (σ) of a material is defined as the reciprocal of its resistivity (ρ). Therefore, we can express this relationship as:
σ=1ρ
- The resistivity (ρ) can be defined in terms of electric field intensity (E) and current density (J). According to the definition, resistivity is given by:
ρ=EJ
- Here, E is the electric field intensity and J is the current density at a point inside the conductor.
- Now, substituting the expression for resistivity (ρ) into the equation for conductivity (σ):
σ=1ρ=1EJ=JE
- From the above equation, we can rearrange it to express current density (J) in terms of conductivity (σ) and electric field intensity (E):
J=σ⋅E
Thus, the relation between current density (J), conductivity (σ), and electric field intensity (E) for a metallic conductor is:
J=σ⋅E
Similar Questions
what is the relation between Mass and density.
View SolutionThe electric intesity E, current density j and conductivity σ are related as:
View SolutionDefine the term 'drift velocity' of electrons in a current carrying conductor. Obtain the relationship between the current density and the drift velocity of electrons.
View SolutionThe ratio of magnitude of current density and magnitude of electric field inside the conductor is
View Solution(a) Define the term 'conductivity' of a metallic wire. Write its SI unit.
(b) Using the concept of free electrons in a conductor, derive the expression for the conductivity of a wire in te'rms of number density and relaxation time. Hence obtain the relation between current density and the applied electric field E.
View SolutionA chargo q is uniformly distributed on a ring-shaped conductor of radius a. Find the field potential in an arbitrary point on the conductor's axis a distance I away from the plane in which the conductor lies. Using the relation between the potential and the field intensity, find the field intensity at this point.
View SolutionWhat is current density? Write the vector equation connecting current density J with electric field intensity E for an ohmic conductor.
View SolutionA electric current passes through non uniform cross-section wire made of homogeneous and isotropic material. If the JA and JB be the current densities and EA and EB be the electric field intensities at A and B respectively, then
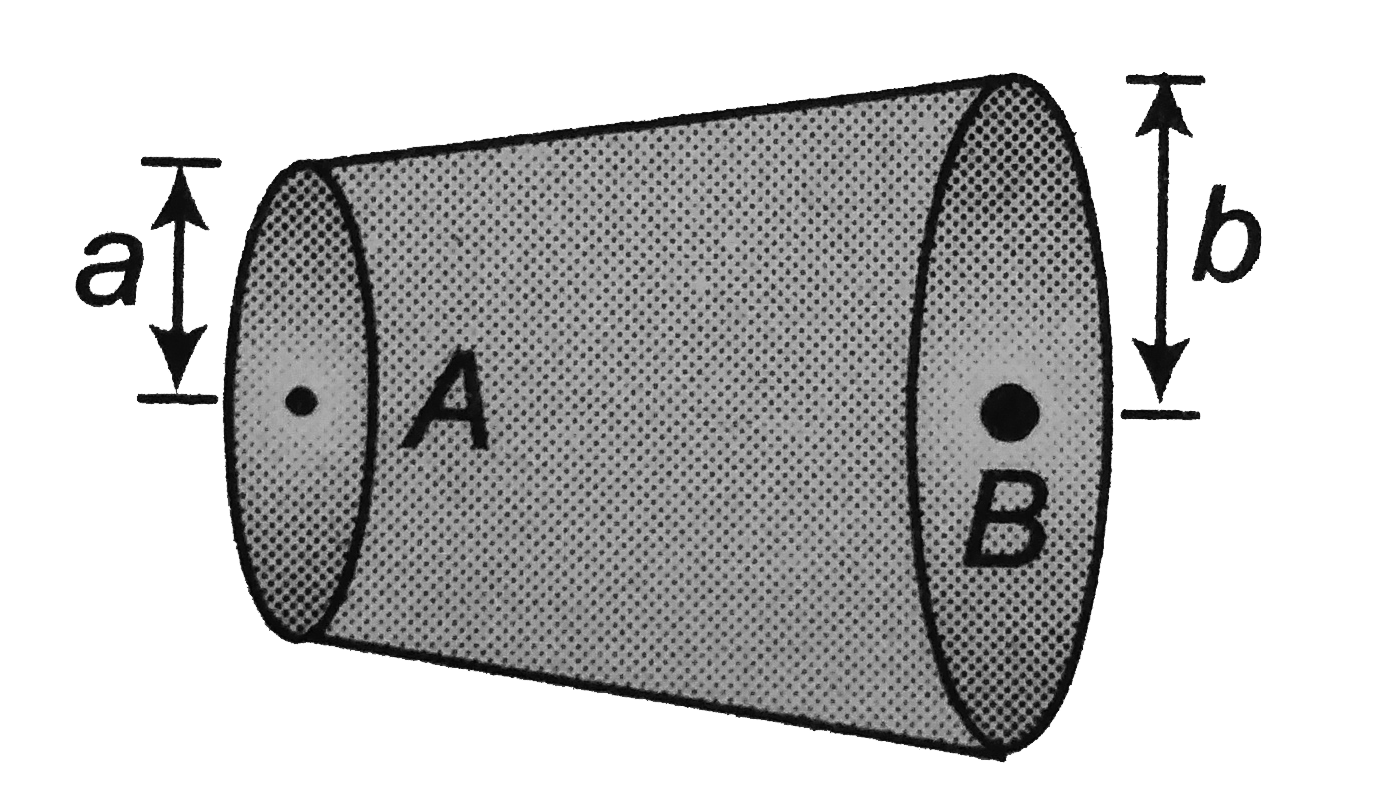
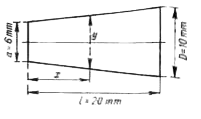
View SolutionA current of 100 A flows in a conical copper with dimensions as shown in Fig 26.8. Find the current density and electric field intensity at the end faces of the conductor
View Solutiona. A steady current flows in a metallic conductor of non - uniform cross section. State which of the quantities i.e., current density, electric field, and drift velocity remain constant?
b. A steady current passes through a cylindrical conductor. Is there an electorn field inside the conductor?
View Solution
