The given figure shows parallelogram ABCD. Points M and N lie in diagonal BD such that DM=BN
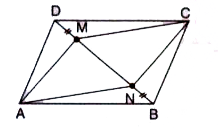 .
.
Prove that:
(i) ΔDMC≅ΔBNA and so CM=AN.
(ii) ΔAMD≅ΔCNB and so AM=CN.
(iii) ANCM is a parallelogram.
Step by step video & image solution for The given figure shows parallelogram ABCD. Points M and N lie in diagonal BD such that DM=BN . Prove that: (i) DeltaDMCcong DeltaBNA and so CM=AN. (ii) DeltaAMDcongDeltaCNB and so AM=CN. (iii) ANCM is a parallelogram. by Maths experts to help you in doubts & scoring excellent marks in Class 8 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
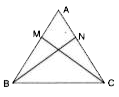
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP=BQ. Show that:
(i) ΔAPD≅ΔCQB
(ii) AP=CQ
(iii) ΔAQB≅ΔCPD
(iv) AQ=CP
(v) APCQ is a parallelogram.

View SolutionThe given figure shows a parallelogram ABCD with area 324sq. cm. P is a point in AB such that AP:PB= 1:2. Find the area of ΔAPD.
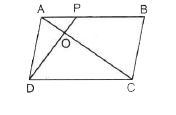
View Solution
Knowledge Check

The given figure shows a parallelogram ABCD whose diagonals intersect each other at point O. if OB=6 cm and AC is 6 cm more than BD, find OC.A12cmB10cmC9cmD11cm
In the given figure, ABCD is a parallelogram in which AN and CP are perpendiculars on diagonal BD. Prove that :
(i) ΔADN=ΔCBP
(ii)AN=CP
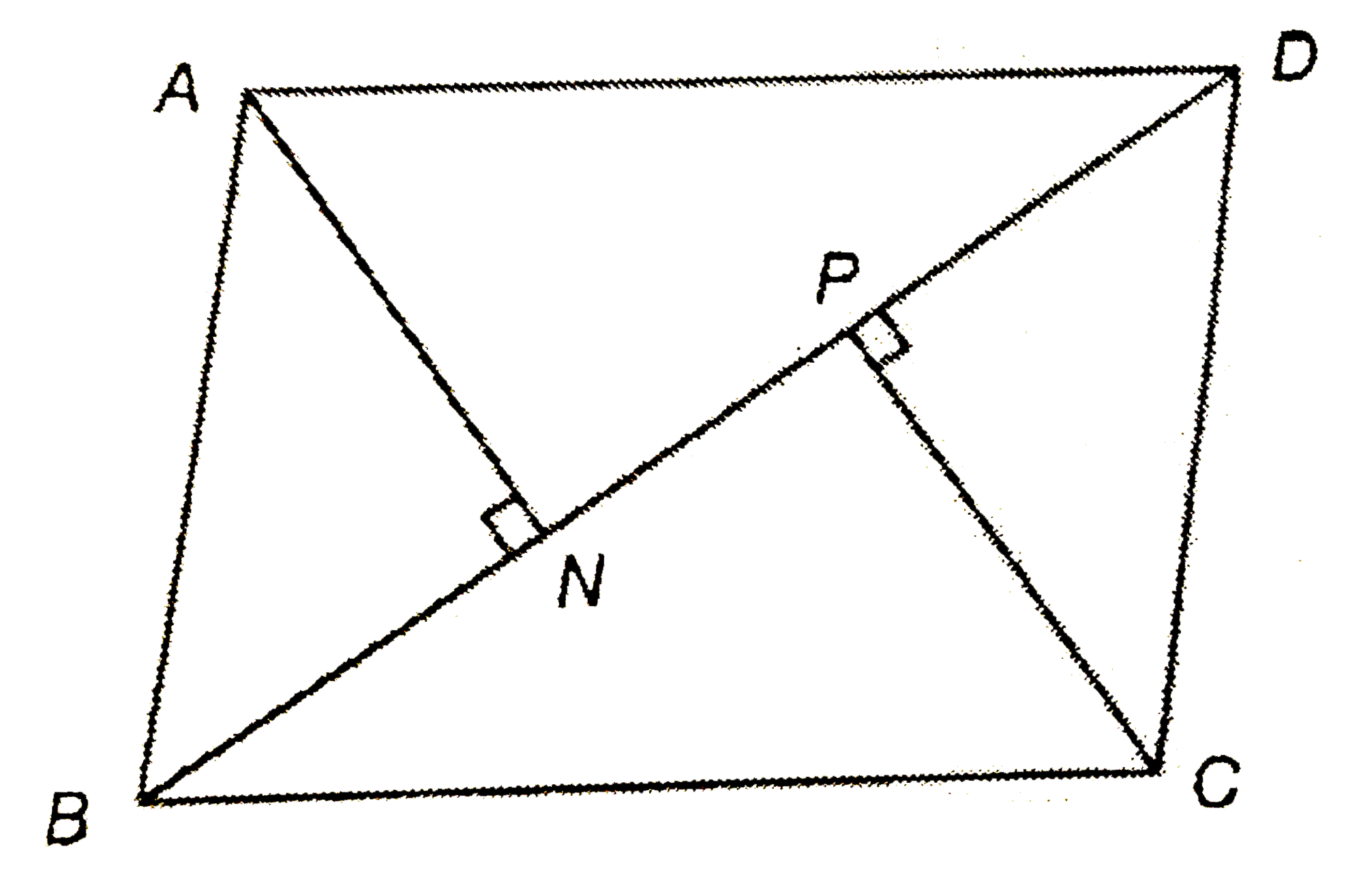
View SolutionIn the adjoining figure ABCD is a parallelogram, ABM is a line segment and E is the mid-point of BC. Prove that :
(i) ΔDCE≅ΔMBe (ii) AB=BM
(iii) AM=2DC
View SolutionIn parallelogram ABCD two points P and Q are taken on diagonal BD such that DP = BQ (set figure). Show that:
(i)ΔAPD≅CQB(ii)AP=CQ(iii)ΔAQB≅ΔCPD(iv)AQ=CP(v)APCQis a parallelogram. ltbegt
View SolutionThe given figure shows a parallelogram ABCD. Squares ABPQ and ADRS are drawn on sides AB and AD of the parallelogram ABCD. Prove that :
(i) ∠SAQ=∠ABC
(ii) SQ = AC

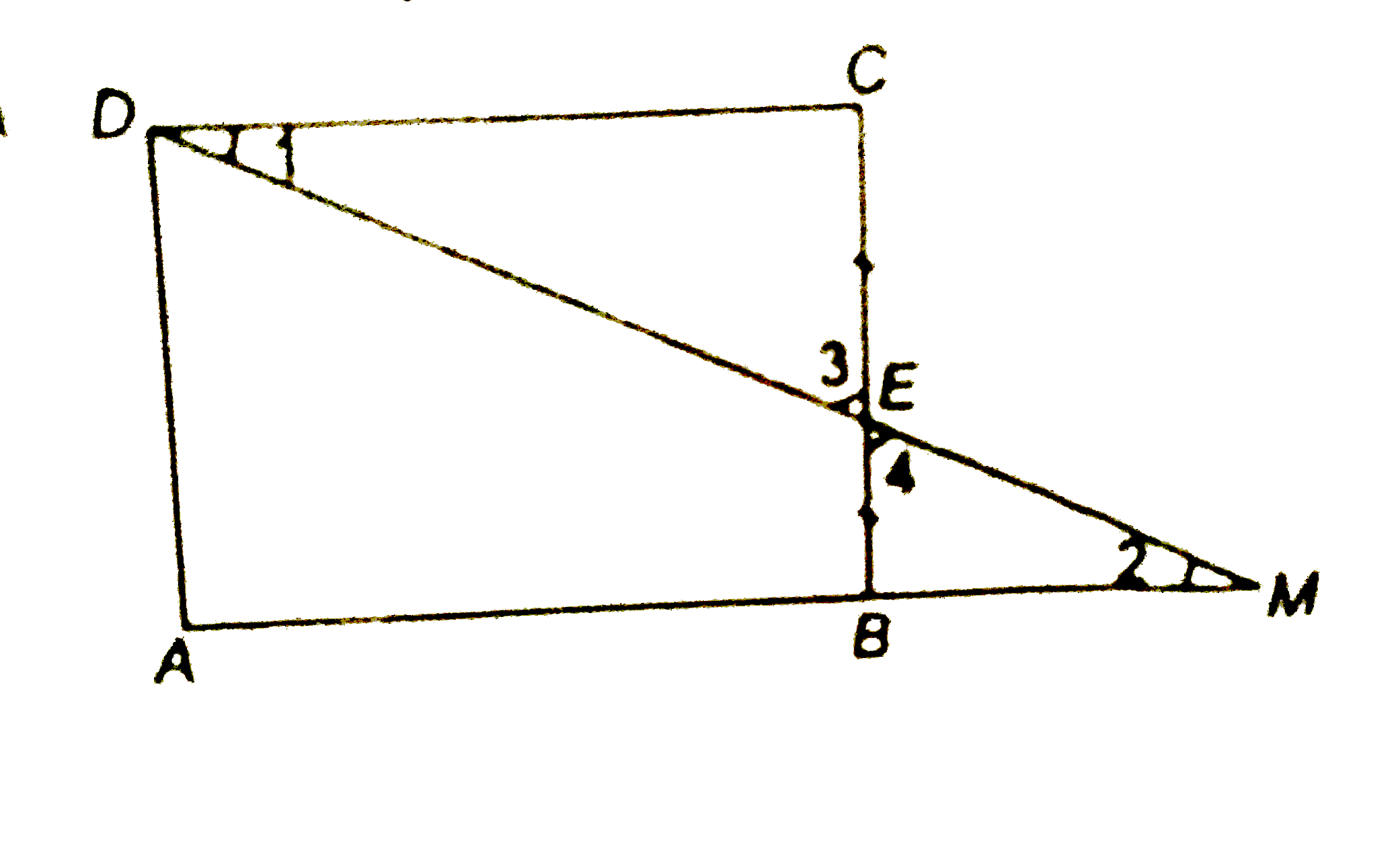
View SolutionThe following figure shows a triangle ABC in which AB=AC. M is a point on AB and N is a point on AC such that BM = CN. Prove that
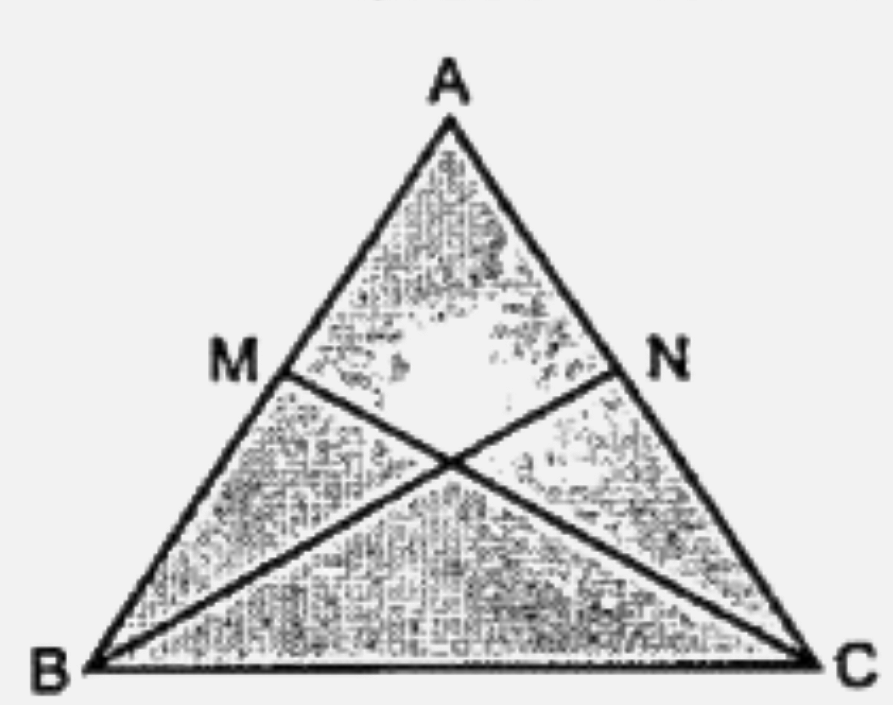
BN=CM
View SolutionThe following figure shows a triangle ABC in which AB=AC. M is a point on AB and N is a point on AC such that BM = CN. Prove that
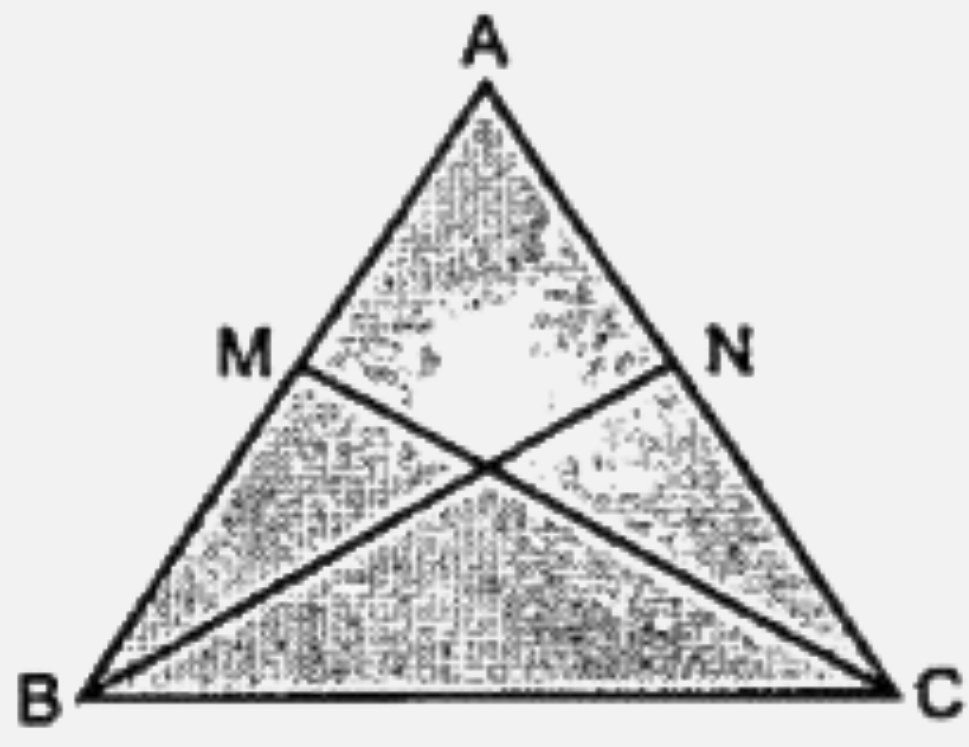
AM=AN
View SolutionThe following figure shows a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN. Prove that :
(i) AM = AN
(ii) ΔAMC≅ΔANB
(iii) BN = CM
(iv) ΔBMC≅ΔCNB
View Solution
