Question

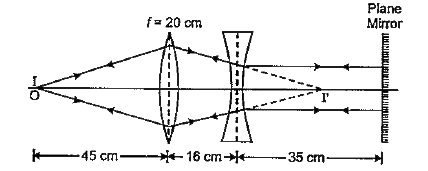
The following figure shows the positions of a point object O, two lenses, a Plane mirror and the final image I which coincides with the object. The focal length of the convex lens is 20 cm. Calculate the focal length of the concave lens.

The distance between the first and the sixth bright fringes formed in Young's double slit experiment ( measured by a spectrometer ) is found to be 12.5 mm. The separation between the slits is 0.12 mm and the distance of the screen from the slits is 60 cm. Calculate :
The fringes width

Explanation

Step-by-Step Solution

1. Identify Given Data:
- Focal length of the convex lens, \( f_1 = +20 \, \text{cm} \)
- Distance from object \( O \) to convex lens \( = 45 \, \text{cm} \) (denote as \( u_1 = -45 \, \text{cm} \) since it is on the same side as the object)
- Distance from convex lens to concave lens \( = 16 \, \text{cm} \)
- Distance from convex lens to plane mirror \( = 35 \, \text{cm} \)

2. Use the Lens Formula for the Convex Lens:
\( \frac{1}{f} = \frac{1}{v} - \frac{1}{u} \)
Rearranging gives:
\( \frac{1}{v} = \frac{1}{f} + \frac{1}{u} \)
Substituting the values:
\( \frac{1}{v} = \frac{1}{20} + \frac{1}{-45} \)

3. Calculate \( v \):
\( \frac{1}{v} = \frac{45 - 20}{900} = \frac{25}{900} = \frac{1}{36} \)
Therefore, \( v = 36 \, \text{cm} \).

4. Determine the Object Distance for the Concave Lens:
The distance from the convex lens to the concave lens is \( 16 \, \text{cm} \), so:
\( u_2 = v - 16 = 36 - 16 = 20 \, \text{cm} \quad (\text{object distance for concave lens, taken as negative}) \)
Thus, \( u_2 = -20 \, \text{cm} \).

5. Use the Lens Formula for the Concave Lens:
For the concave lens, we have:
\( \frac{1}{f_2} = \frac{1}{v} - \frac{1}{u_2} \)
Since the image formed by the concave lens is virtual, \( v \) is considered to be at infinity:
\( \frac{1}{f_2} = 0 - \frac{1}{-20} \)
Thus:
\( \frac{1}{f_2} = \frac{1}{20} \)
Therefore, \( f_2 = -20 \, \text{cm} \).

Part 2: Calculating the Fringe Width in Young's Double Slit Experiment

1. Identify Given Data:
- Distance between the first and sixth bright fringes \( = 12.5 \, \text{mm} = 12.5 \times 10^{-3} \, \text{m} \)
- Separation between the slits \( d = 0.12 \, \text{mm} = 0.12 \times 10^{-3} \, \text{m} \)
- Distance from the slits to the screen \( D = 60 \, \text{cm} = 0.6 \, \text{m} \)

2. Relate Fringe Positions:
The position of the \( n \)-th bright fringe is given by:
\( x_n = \frac{n \lambda D}{d} \)
Therefore, the distance between the sixth and first bright fringes is:
\( x_6 - x_1 = \frac{6 \lambda D}{d} - \frac{1 \lambda D}{d} = \frac{5 \lambda D}{d} \)

3. Set Up the Equation:
\( \frac{5 \lambda D}{d} = 12.5 \times 10^{-3} \)

4. Solve for Fringe Width:
The fringe width \( \beta \) is given by:
\( \beta = \frac{\lambda D}{d} \)
From the previous equation:
\( 5 \beta = 12.5 \times 10^{-3} \)
Thus:
\( \beta = \frac{12.5 \times 10^{-3}}{5} = 2.5 \times 10^{-3} \, \text{m} = 2.5 \, \text{mm} \)

Final Answers:
- Focal length of the concave lens: \( f_2 = -20 \, \text{cm} \)
- Fringe width: \( \beta = 2.5 \, \text{mm} \)