A 30 μF capacitor, 0.2 H inductor and a 50 Ω resistor are connected in series to an a.c. Source whose emf is given by E = 310 sin (314 t) where E is in volt and t is in second. Calculate :
The impedance of the circuit and
To calculate the impedance of the circuit consisting of a capacitor, inductor, and resistor connected in series, we can follow these steps:
Step 1: Identify the given values
- Capacitance, C=30μF=30×10−6F
- Inductance, L=0.2H
- Resistance, R=50Ω
- The equation for the emf is given as E=310sin(314t).
Step 2: Determine the angular frequency
From the emf equation, we can identify the angular frequency ω:
- ω=314rad/s
Step 3: Calculate the inductive reactance XL
The inductive reactance is given by the formula:
XL=ωL
Substituting the values:
XL=314×0.2=62.8Ω
Step 4: Calculate the capacitive reactance XC
The capacitive reactance is given by the formula:
XC=1ωC
Substituting the values:
XC=1314×30×10−6=10.00942≈106.15Ω
Step 5: Calculate the impedance Z
The impedance Z in an RLC series circuit is given by:
Z=√R2+(XL−XC)2
Substituting the values:
Z=√502+(62.8−106.15)2
Calculating XL−XC:
XL−XC=62.8−106.15=−43.35
Now, substituting back into the impedance formula:
Z=√2500+(−43.35)2
Calculating (−43.35)2:
(−43.35)2≈1875.2225
Now, substituting this value:
Z=√2500+1875.2225=√4375.2225≈66.18Ω
Final Answer
The impedance of the circuit is approximately Z≈66.18Ω.
---
- Capacitance, C=30μF=30×10−6F
- Inductance, L=0.2H
- Resistance, R=50Ω
- The equation for the emf is given as E=310sin(314t).
From the emf equation, we can identify the angular frequency ω:
- ω=314rad/s
The inductive reactance is given by the formula:
XL=ωL
Substituting the values:
XL=314×0.2=62.8Ω
The capacitive reactance is given by the formula:
XC=1ωC
Substituting the values:
XC=1314×30×10−6=10.00942≈106.15Ω
The impedance Z in an RLC series circuit is given by:
Z=√R2+(XL−XC)2
Substituting the values:
Z=√502+(62.8−106.15)2
Calculating XL−XC:
XL−XC=62.8−106.15=−43.35
Now, substituting back into the impedance formula:
Z=√2500+(−43.35)2
Calculating (−43.35)2:
(−43.35)2≈1875.2225
Now, substituting this value:
Z=√2500+1875.2225=√4375.2225≈66.18Ω
The impedance of the circuit is approximately Z≈66.18Ω.
Similar Questions
A 20 μF capacitor, 0.2 H inductor and a 50 Ω resistor are connected in series to an a.c. Source whose emf is given by E = 310 sin (314 t) where E is in volt and t is in second. Calculate :
peak value of current in the circuit.
View SolutionA 25(μ)F capacitor, a 0.1 H inductor and a 25Ω resistor are connected in series with an ac source of emf E=310sin314t. Find
(a) the frequency of the emf
(b) the impedance of the circuit
(c) the current in the circuit.
(d) the phase angle
View SolutionA 0.21 H inductor and a 12Ω resistance are connected in series to a 220 V, 50 Hz ac source.
The current in the circuit is
View SolutionA 50μF capacitor, a 30Ω esistor and a 0.7 H inductor are connected in series to an a.c. supply which generates an emf .e. given by e = 300 sin (200 t) volt. Calculate peak value of the current flowing through the circuit.
View SolutionA coil of inductance 0.01 H is connected in series with a capacitor of capacitance 25μF with an AC source whose emf is given by E = 310 sin 314t (volt). What is the reactance of the circuit ?
View SolutionA satellite is launched into a circular orbit of radius R around the earth while a second satellite is launched into an orbit of radius 1.02R. The percentage difference in the time period is:
View SolutionA 0.01 H inductor and √3πΩ resistance are connected in series with a 220 V, 50 Hz AC source. The phase difference between the current and emf is
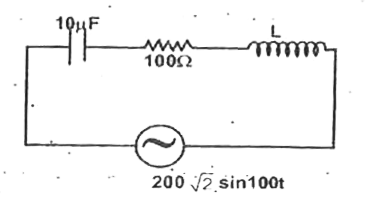
View SolutionA 10 muF capacitor, an inductor and a resistor of 100Omega are connected to an alternating source of emf 200sqrt2 sin 100t as shown in the figure. What is the r.m.s current in the circuit and the value of the inductance if the current and the source voltage attain their maxima simultaneously? What is the average power consumed in this case
View SolutionAn inductor 20mH, a capacitor 50μF and a resistor 40Ωare connected in series across of emf V=10sin340t. The power loss in A.C. circuit is
View SolutionAn inductor 2/π Henry, a capacitor 100/TμF and a resistor 75Ω are connected in series across a source of emf V=10sin100πt. Here t is in second. (a) find the impedance of the circuit. (b) find the energy dissipated in the circuit in 20 minutes.
View Solution
