A 25(μ)F capacitor, a 0.1 H inductor and a 25Ω resistor are connected in series with an ac source of emf E=310sin314t. Find
(a) the frequency of the emf
(b) the impedance of the circuit
(c) the current in the circuit.
(d) the phase angle
(a) Given ω=314⇒2πf=314⇒f=50Hz
(b) Impendance of the circuit is
Z=√R2+(XC_XL)2=√252+962=99.2Ω
(c) We have to find rms current in hte circuit in the current . It is given by
Iv=EvZ=310/√299.2=2.21A
(d) Let ϕ be the angle by which current leads emf, then
tan(ϕ)=XC−XLR=9625⇒ϕ=75.4∘
Topper's Solved these Questions
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercise 5.1
15 Videos
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercises Subjective
15 Videos
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Single Correct
10 Videos
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - ddp.4.3
15 Videos
Similar Questions
A 30 μF capacitor, 0.2 H inductor and a 50 Ω resistor are connected in series to an a.c. Source whose emf is given by E = 310 sin (314 t) where E is in volt and t is in second. Calculate :
The impedance of the circuit and
View SolutionA 20 μF capacitor, 0.2 H inductor and a 50 Ω resistor are connected in series to an a.c. Source whose emf is given by E = 310 sin (314 t) where E is in volt and t is in second. Calculate :
peak value of current in the circuit.
View Solution
Knowledge Check
A circuit containing a 20Ω resistor and 0.1μF capacitor in series is connected to 320 V ac supply of angular frequency 100 rad s−1. The impedance of the circuit is
A105ΩB104ΩC106ΩD1010Ω
A 0.21 H inductor and a 12Ω resistance are connected in series to a 220 V, 50 Hz ac source.
The current in the circuit is
View SolutionA satellite is launched into a circular orbit of radius R around the earth while a second satellite is launched into an orbit of radius 1.02R. The percentage difference in the time period is:
View SolutionAn inductor 2/π Henry, a capacitor 100/TμF and a resistor 75Ω are connected in series across a source of emf V=10sin100πt. Here t is in second. (a) find the impedance of the circuit. (b) find the energy dissipated in the circuit in 20 minutes.
View SolutionAnswer the following:
(a) What do you understand by 'sharpness of resonance' for a series LCR resonant circuit? How is it related with the quality factor 'Q' of the circuit? Using the graphs given in the diagram, explain the factors which affect it. For which graph is the resistance (R ) minimum?
(b) A 2μF capacitor, 100Ω resistor and 8H inductor are connected in series with an ac source. Find the frequency of the ac source for which the current drawn in the circuit is maximum.
If the peak value of emf of the source is 200 V, calculate the (i) maximum current, and (ii) inductive and capacitive reactance of the circuit at resonance.
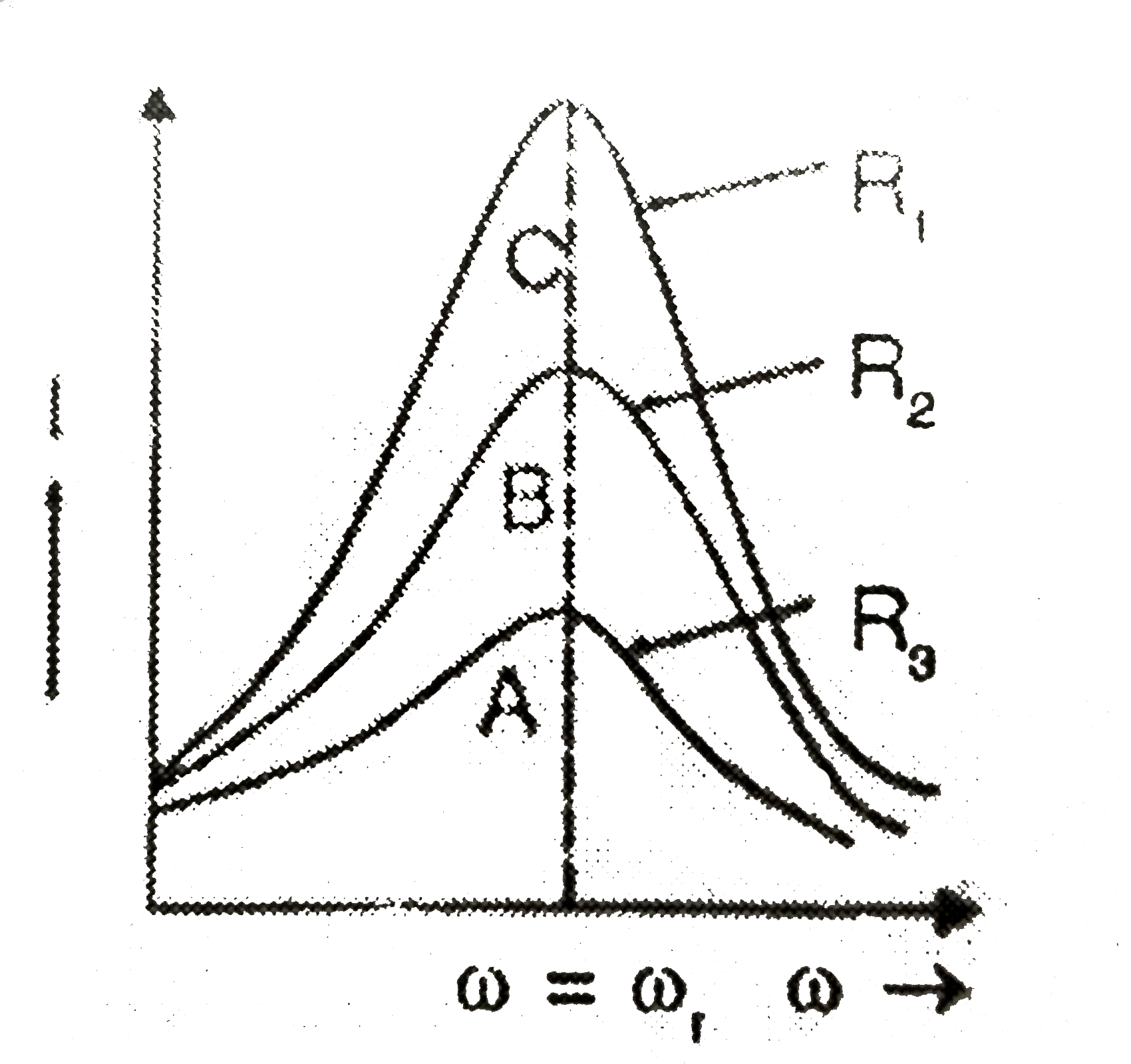
View SolutionAn inductor 20×10−3 a capacitor 100(μ)F and a resistor 50Ω are connected in series across a source of emf V=10sin314t.
Then the energy dissipated in the circuit in 20 mim is
View SolutionA 0.01 H inductor and √3πΩ resistance are connected in series with a 220 V, 50 Hz AC source. The phase difference between the current and emf is
View SolutionAn 8 H inductor, a 2 μF capacitor and a 100 Ω resistor are connected in series to an A.C. supply of 220 V and 50 Hz. Calculate :
(i) Impedance of the circuit.
(ii) Current flowing through the circuit.
(iii)Phase difference between the current and the supply voltage.
(iv) Average power consumed by the circuit.
View Solution
