The value of r when the regression lines are perpendicular to each other is:
0
1
2
3
To find the value of r when the regression lines are perpendicular to each other, we can follow these steps:
Step 1: Understand the relationship between regression lines and correlation coefficient
The regression lines of two variables X and Y are given by their equations. The angle θ between these regression lines can be expressed in terms of the correlation coefficient r.
Step 2: Use the formula for the angle between regression lines
The formula relating the angle θ between the regression lines to the correlation coefficient r is:
tanθ=1−r2r⋅σxσy
where σx and σy are the standard deviations of X and Y respectively.
Step 3: Set the angle for perpendicular lines
If the regression lines are perpendicular, then θ=π2. Therefore, we have:
tan(π2)=∞
Step 4: Set up the equation
From the above relationship, we can set:
1−r2r⋅σxσy=∞
This implies that the denominator must be zero since a finite number divided by zero approaches infinity.
Step 5: Solve for r
To make the denominator zero, we can set:
r⋅σx+r⋅σy=0
Since σx and σy are both standard deviations and cannot be zero, we can conclude that:
r=0
Conclusion
Thus, the value of r when the regression lines are perpendicular to each other is:
0
The regression lines of two variables X and Y are given by their equations. The angle θ between these regression lines can be expressed in terms of the correlation coefficient r.
The formula relating the angle θ between the regression lines to the correlation coefficient r is:
tanθ=1−r2r⋅σxσy
where σx and σy are the standard deviations of X and Y respectively.
If the regression lines are perpendicular, then θ=π2. Therefore, we have:
tan(π2)=∞
From the above relationship, we can set:
1−r2r⋅σxσy=∞
This implies that the denominator must be zero since a finite number divided by zero approaches infinity.
To make the denominator zero, we can set:
r⋅σx+r⋅σy=0
Since σx and σy are both standard deviations and cannot be zero, we can conclude that:
r=0
Thus, the value of r when the regression lines are perpendicular to each other is:
0
Topper's Solved these Questions
- SELF ASSESSMENT PAPER 04BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 04EXERCISE - SECTION .B.
10 Videos
- SELF ASSESSMENT PAPER 03BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 03EXERCISE - Section -C
10 Videos
- SELF ASSESSMENT PAPER 05BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 05EXERCISE - SECTION .C.
12 Videos
Similar Questions
Knowledge Check
The two line of regression are perpendicular if
Abyx.bxy=1Bbyx.bxy=−1Cbxy.byx=0Dbxy+byx=0
Which of the following statements are true (T) and which are false (F)? Give reasons.
(i)If two lines are intersected by a transversal, then corresponding angles are equal.
(ii)If two parallel lines are intersected by a transversal, then alternate interior angles are equal.
(iii)Two lines perpendicular to the same line are perpendicular to each other.
(iv)Two lines parallel to the same line are parallel to each other.
(v)If two parallel lines are intersected by a transversal, then the interior angle on the same side of the transversal are equal.
View SolutionTwo equal electroic currents are flowing perpendicular to each other as shown oin the figure. AB and CD are perpendicular to each other and symeetrically placed w.r.t the currents, where do we except the resultant magnetic field to be zero ?
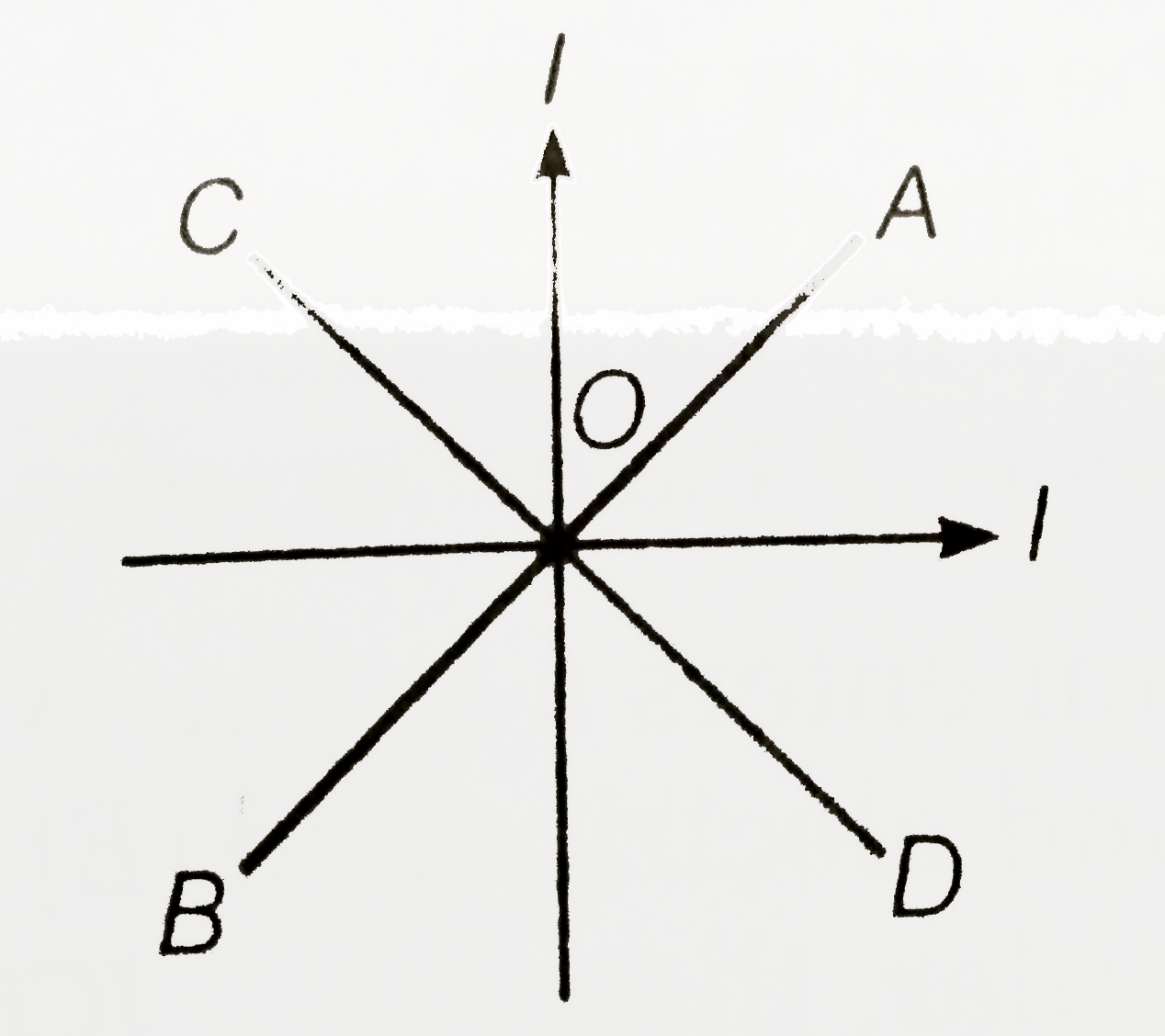
View SolutionShow that the diagonals of a rhombus are perpendicular to each other
View SolutionShow that the diagonals of a rhombus are perpendicular to each other
View SolutionState parallelogram law of vector addition. Find analytically the magnitude and direction of resultant vector. Apply it to find the resultant when,
(i) Two vectors are parallel to each other
(ii) Two vectors are perpendicular to each other
View SolutionTwo straight lines are cut by a transversal. If the bisectors of a pair of co-interior angles are perpendicular to each other , prove the two straight lines are parallel to each other.
View Solution(A) : In electromagnetic waves electric field and magnetic field lines are perpendicular to each other. (R) : Electric field and magnetic field are self sustaining.
View Solution
