We know that parallelogram is also a quadrilateral. Let us split such quadrilateral into two triangles. Find their areas and subsequently that of the parallelogram. Does this process in turn with the formula that you already know?Solution in Telugu
Step by step video & image solution for We know that parallelogram is also a quadrilateral. Let us split such quadrilateral into two triangles. Find their areas and subsequently that of the parallelogram. Does this process in turn with the formula that you already know? by Maths experts to help you in doubts & scoring excellent marks in Class 8 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Find the product of 5x, 6y and 7z.
View SolutionA cycle is marked at ₹3600 and sold for ₹3312. What is the discount and discount percentage?
View SolutionThe area of parallelogram; triangle and quadrilateral in terms of cross product.
View SolutionIf each diagonals of a quadrilateral separates it into two triangles of equal area then show that the quadrilateral is a parallelogram.
View Solutionयदि किसी चतुर्भुज का प्रत्येक विकर्ण इसे दो समान क्षेत्रफल वाले त्रिभुजों में विभक्त करे, तो सिद्ध कीजिए कि यह चतुर्भुज समान्तर चतुर्भुज है।
View Solutionचित्र में BD चतुर्भुज ABCD का विकर्ण है। सिद्ध कीजिए कि ABCD एक समांतर चतुर्भुज है तथा समांतर चतुर्भुज ABCD का क्षेत्रफल भी ज्ञात कीजिए।

View Solutionहम जानते है कि समांतर चतुर्भुज भी एक चतुर्भुज है | आइए, इसे भी हम दो त्रिभुजों में विभक्त करते है और इन दोनों त्रिभुजों का क्षेत्रफल ज्ञात करते है | इस प्रकार समांतर चतुर्भुज का क्षेत्रफल भी ज्ञात करते है | क्या यह सूत्र आपको पूर्व में ज्ञात सूत्र से मेल खता है ? ( आकृति 11.12 )
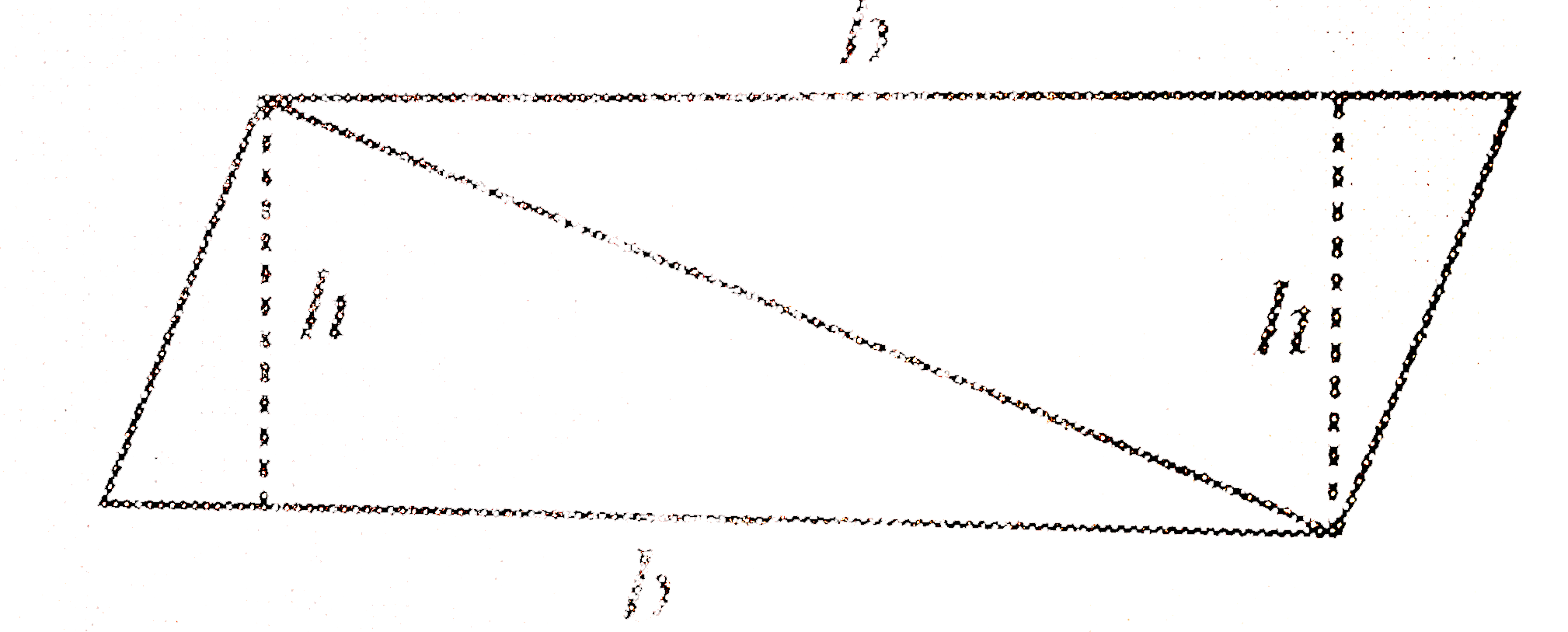
View Solution(a) यदि किसी चतुर्भुज का प्रत्येक विकर्ण इसे बराबर क्षेत्रफल वाले दो त्रिभुजों में बाटता हो तो सिद्ध कीजिए की वह चतुर्भुज एक समांतर चतुर्भुज होता है।
(b) यदि किसी चतुर्भुज के विकर्ण चतुर्भुज को बराबर क्षेत्रफल वाले चार त्रिभुजों में बाटे तो सिद्ध करे की वह एक समांतर चतुर्भुज होगा।
View SolutionWhen proving that a quadrilateral is a parallelogram by using slopes you must find
View SolutionProve that if each diagonal of a quadrilateral bisects it into two triangles of equal areas, then it is a parallelogram.
View SolutionIf each diagonals of a quadrilateral separates it into two triangles of equal area then show that the quadrilateral is a parallelogram.
View SolutionWe know that parallelogram is also a quadrilateral. Let us also split such a quadrilateral into two triangles, find their areas ad hence that of the parallelogram . Does this agree with the formula that you know already?
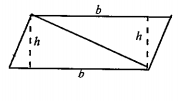
View SolutionIf each diagonals of a quadrilateral separates it into two triangles of equal area then show that the quadrilateral is a parallelogram.
View SolutionABCD is a quadrilateral and BD is one of its diagonals, as shown in the figure. Prove that quadrilateral ABCD is a parallelogram, also find its area.
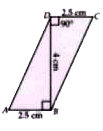
View Solution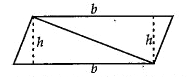
We know that parallelogram is also a quadrilateral. Let us also split such a quadrilateral into two triangles. Find their areas and hence that of the parallelogram. Does this agree with the formula that you know already?
View Solution
