In ΔABC, D, E are the mid points ¯¯¯¯¯¯AB,¯¯¯¯¯¯AC of F, G are the mid points of ¯¯¯¯¯¯AD,¯¯¯¯¯¯AE.If ¯¯¯¯¯¯FG=2cm, then BC=Solution in Telugu
10 cm.
4 cm.
6cm.
8 cm.
Step by step video & image solution for In DeltaABC, D, E are the mid points bar(AB),bar(AC) of F, G are the mid points of bar(AD),bar(AE).If bar(FG)= 2cm, then BC= by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Can you give any two axioms from your daily life.
View Solution
In the above figure (not to scale), E and F are the mid points of AB and CD respectively.
¯¯¯¯¯¯AB∣∣∣∣¯¯¯¯¯¯CD,¯¯¯¯¯¯BC∣∣∣∣¯¯¯¯¯¯AD,∠ADE=70∘, AND ∠BCE=40∘,∠DEC is
View SolutionM and N are mid-point of the diagnols AC and BD respectivley of quadrilateral ABCD, then¯¯¯¯¯¯AB+¯¯¯¯¯¯AD+¯¯¯¯¯¯CB+¯¯¯¯¯¯CD=
View SolutionIf D is the mid -point of side AB of ΔABC, then ¯¯¯¯¯¯AB+¯¯¯¯¯¯BC+¯¯¯¯¯¯AC=
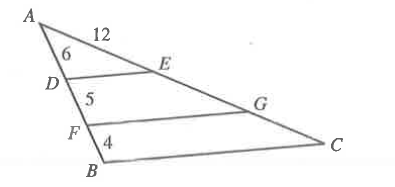
View SolutionIn the figure shown below, E and G lie on ¯¯¯¯¯¯AC, D and F lie on ¯¯¯¯¯¯AB,¯¯¯¯¯¯DEand¯¯¯¯¯¯FG are parallel to ¯¯¯¯¯¯BC, and the given lengths are in feet. What is the length of ¯¯¯¯¯¯AC, in feet?
View SolutionIn ΔABC, P, Q and R are mid points of the sides AB, BC, and CA respectively. If D is any point
i) then express ¯¯¯¯¯¯DA+¯¯¯¯¯¯DB+¯¯¯¯¯¯DC in terms of ¯¯¯¯¯¯DP,¯¯¯¯¯¯DQand¯¯¯¯¯¯DR
ii) If ¯¯¯¯¯¯PA+¯¯¯¯¯¯QB+¯¯¯¯¯¯RC=¯a then find ¯a.
View SolutionIf AD, BE and CF are the medians of ΔABC, then the value of ¯¯¯¯¯¯BC.¯¯¯¯¯¯AD+¯¯¯¯¯¯CA.¯¯¯¯¯¯BE+¯¯¯¯¯¯AB.¯¯¯¯¯¯CF=
View SolutionIn ΔABC, if D is the midpoint of BC then prove that ¯¯¯¯¯¯AD=¯¯¯¯¯¯AB+¯¯¯¯¯¯AC2
View SolutionOABC is a tetrahedron D and E are the mid points of the edges ¯¯¯¯¯¯OAand¯¯¯¯¯¯BC. Then the vector ¯¯¯¯¯¯DE in terms of ¯¯¯¯¯¯OA,¯¯¯¯¯¯OB and ¯¯¯¯¯¯OC.
View SolutionIn ΔABC, P, Q and R are mid points of the sides AB, BC, and CA respectively. If D is any point
i) then express ¯¯¯¯¯¯DA+¯¯¯¯¯¯DB+¯¯¯¯¯¯DC in terms of ¯¯¯¯¯¯DP,¯¯¯¯¯¯DQand¯¯¯¯¯¯DR
ii) If ¯¯¯¯¯¯PA+¯¯¯¯¯¯QB+¯¯¯¯¯¯RC=¯a then find ¯a.
View SolutionIf D, E and F are respectively the mid-points of AB, AC and BC in ΔABC then ¯¯¯¯¯¯BE+¯¯¯¯¯¯AF=
View SolutionABCDE is a pentagon then
¯¯¯¯¯¯AB+¯¯¯¯¯¯AE+¯¯¯¯¯¯BC+¯¯¯¯¯¯DC+¯¯¯¯¯¯ED+¯¯¯¯¯¯AC=
View SolutionIf D, E, F are mid points of sides BC, CA, AB of triangle ABC and G is centroid then
List-IList-IIA) ¯¯¯¯¯¯AD+¯¯¯¯¯¯BE+¯¯¯¯¯¯CF1) ¯¯¯¯¯¯CBB) ¯¯¯¯¯¯GA+¯¯¯¯¯¯GB2) 3¯¯¯¯¯¯OGC) ¯¯¯¯¯¯AB+¯¯¯¯¯¯CA3) ¯¯¯OD) ¯¯¯¯¯¯OD+¯¯¯¯¯¯OE+¯¯¯¯¯¯OF4) −23(¯¯¯¯¯¯AD+¯¯¯¯¯¯BE)5) 3¯¯¯¯¯OI
The correct matching is
View SolutionIn ΔABC, if BC=a,CA=bandAB=C, then what is the value of ¯¯¯¯¯¯AB.¯¯¯¯¯¯AC+¯¯¯¯¯¯BC.¯¯¯¯¯¯BA+¯¯¯¯¯¯CA.¯¯¯¯¯¯CB?
View SolutionIf ¯¯¯¯¯¯AD,¯¯¯¯¯¯BEand¯¯¯¯¯¯CF are the medians of ΔABC, then find the value of ¯¯¯¯¯¯BC.¯¯¯¯¯¯AD+¯¯¯¯¯¯CA.¯¯¯¯¯¯BE+¯¯¯¯¯¯AB.¯¯¯¯¯¯CF.
View Solution
