If AD, BE and CF are the medians of ΔABC, then the value of ¯¯¯¯¯¯BC.¯¯¯¯¯¯AD+¯¯¯¯¯¯CA.¯¯¯¯¯¯BE+¯¯¯¯¯¯AB.¯¯¯¯¯¯CF= Solution in Telugu
0
¯0
1
2
The correct Answer is:A
Step by step video, text & image solution for If AD, BE and CF are the medians of DeltaABC, then the value of bar(BC).bar(AD)+bar(CA).bar(BE)+bar(AB).bar(CF)= by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - CROSS PRODUCT OF TWO VECTORS
17 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - MULTIPLE PRODUCT OF TWO VECTORS
21 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - PROPERTIES OF VECTORS
17 Videos
- 3D-COORDINATE SYSTEMBOOK - AAKASH SERIESCHAPTER - 3D-COORDINATE SYSTEMEXERCISE - PRACTICE EXERCISE
40 Videos
- CHANGE OF AXESBOOK - AAKASH SERIESCHAPTER - CHANGE OF AXESEXERCISE - Practice Exercise
29 Videos
Similar Questions
Let ¯aand¯b be two non-collinear unit vectors. If ¯u=¯a−(¯a.¯b)¯band¯v=¯aׯb, then |¯v|=
View SolutionIf →a,→b,→c are three coplanar vectors, ¯p,¯q,¯r are non-zero vectors then ∣∣ ∣ ∣∣¯p⋅¯a¯p⋅¯b¯p⋅¯c¯q⋅¯a¯q⋅¯b¯q⋅¯c¯r⋅¯a¯r⋅¯b¯r⋅¯c∣∣ ∣ ∣∣=
View SolutionLet p¯i+3¯j+4¯kand√q¯i+5¯k be two vectors where p,q≥0 are two scalars. If (p, q) is a pair of values for which their lengths are equal, then there can be
View SolutionThe point (-1,4,-2) lie in the octant
View SolutionThe coordinates of the point (3,-5) in the new system when the origin is shifted to (-2,3) are
View SolutionIn DeltaABC, |bar(CB)| = a, |bar(CA)| = b and |bar(AB)| =c. CD is the median through the vertex C. Then bar(CA).bar(CD)=
View SolutionABC is an equilateral triangle of side ‘a'. Then bar(AB).bar(BC) +bar(BC).bar(CA)+ bar(CA).bar(AB) =
View SolutionIn the given ΔABC,¯¯¯¯¯¯AD,¯¯¯¯¯¯BE and ¯¯¯¯¯¯CF are the medians. G is centroid. What is the ratio of the area of ΔBGD and ΔGCE?
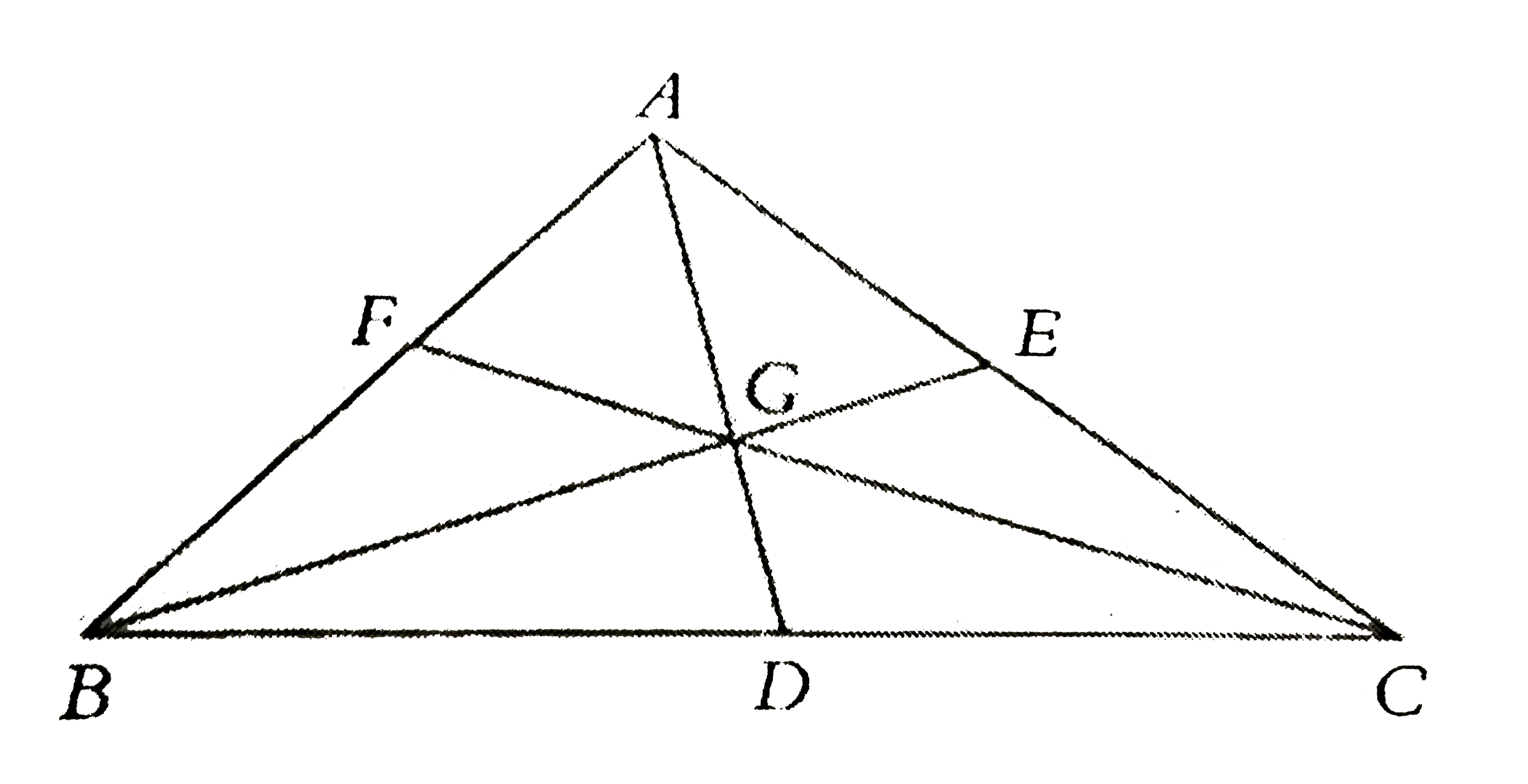
View SolutionIn the above figure (not to scale) bar(AB),bar(BC),bar(CF),bar(DE) and bar(FE) are chords of the circle. If /_ ABC =100^(@) and /_ FED =110^(@) , then /_FPA =
View Solution
In the above ΔABC,¯¯¯¯¯¯AD,¯¯¯¯¯¯BE,and¯¯¯¯¯¯CF are the medians. G is the centroid. What is the ratio of the areas of ΔBGDandΔGCE?
View SolutionD, E, F are the midpoints of the sides BC, CA and AB respectively of △ABC and O is any point in the plane of △ABC. Show that (1)¯¯¯¯¯¯AD+¯¯¯¯¯¯BE+¯¯¯¯¯¯CF=¯0
View SolutionIf AD , BE and CF are medians of ΔABC, then ¯¯¯¯¯¯AD+¯¯¯¯¯¯BE+¯¯¯¯¯¯CF =
View SolutionIf ABCDE is a regular penatagon then :
¯¯¯¯¯¯AB+¯¯¯¯¯¯BC+¯¯¯¯¯¯AD+¯¯¯¯¯¯ED+¯¯¯¯¯¯AE=
View SolutionA,B,C,D are four points in space and ∣∣¯¯¯¯¯¯ABׯ¯¯¯¯¯CD+¯¯¯¯¯¯BCׯ¯¯¯¯¯AD+¯¯¯¯¯¯CAׯ¯¯¯¯¯BD∣∣=λ (area ΔABC) then value of λ is _____
View SolutionIn ΔABC, the bisector of ∠A is ¯¯¯¯¯¯AD.
¯¯¯¯¯¯AD=α¯¯¯¯¯¯AB+β¯¯¯¯¯¯AC, where ……………..
View Solution