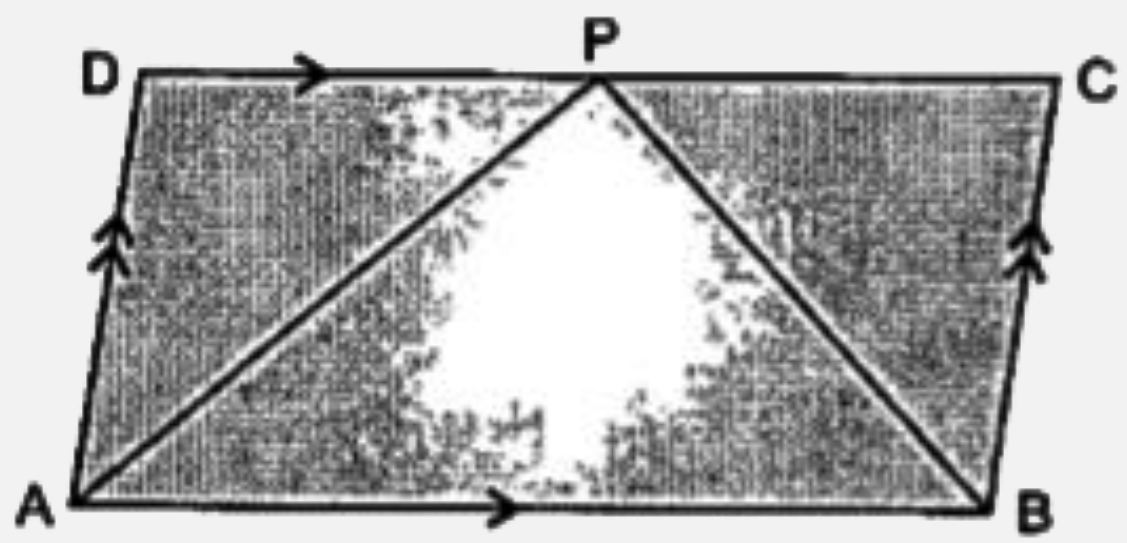
ABCD is a parallelogram in which ∠DAB=80∘. Bisector of ∠Aand∠B meets CD at P. Prove that :

(i) AD = DP
(ii) CP = CB
(iii) DC = 2AB
Step by step video & image solution for ABCD is a parallelogram in which angle DAB = 80^(@). Bisector of angle A and angle B meets CD at P. Prove that : (i) AD = DP (ii) CP = CB (iii) DC = 2AB by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ICSE EXAMINATION PAPER 2020 BOOK - ICSECHAPTER - ICSE EXAMINATION PAPER 2020 EXERCISE - SECTION - B
21 Videos
- GRAPHICAL SOLUTION(SOLUTION OF SIMULTANEOUS LINEAR EQUATIONS, GRAPHICALLY)BOOK - ICSECHAPTER - GRAPHICAL SOLUTION(SOLUTION OF SIMULTANEOUS LINEAR EQUATIONS, GRAPHICALLY)EXERCISE - EXAMPLES
6 Videos
- INDICES (EXPONENTS)BOOK - ICSECHAPTER - INDICES (EXPONENTS)EXERCISE - 4 Marks Questions
9 Videos
Similar Questions
ABCD is a parallelogram in which ∠DAB=80∘. Bisector of ∠Aand∠B meets CD at P. Prove that :
(i) AD = DP
(ii) CP = CB
(iii) DC = 2AD
View SolutionABC is a right triangle with AB = AC.If bisector of ∠A meet BC at D then prove that BC =2 AD .
View SolutionIn parallelogram ABCD, the bisector of angle A meets DC at P and AB = 2AD.
Prove that :
(i) BP bisects angle B.
(ii) Angle APB = 90∘
View SolutionABCD is a quadrilateral in which AB=BC and AD=CD ,Show that BD bisects both the ∠ABC and ∠ADC.
View SolutionIn the adjoining figure, AB>AC and the angle bisectors of ∠B and ∠C meet at point P. Prove that
PB>PC.

View SolutionABCD is a quadrilateral in which AB||DC and AD = BC. Prove that ∠A=∠Band∠C=∠D.
View SolutionIn a tringle ABC, AB = AC and bisector of angle A meets BC at D. Prove that :
(i) ΔABD≅ΔACD (ii) AD is perpendicular to BC.
View SolutionIn triangle ABC , the internal bisector of ∠A∠Band∠C meet at point I . Prove that :
12(AB+BC+CA)<AI+BI+CI
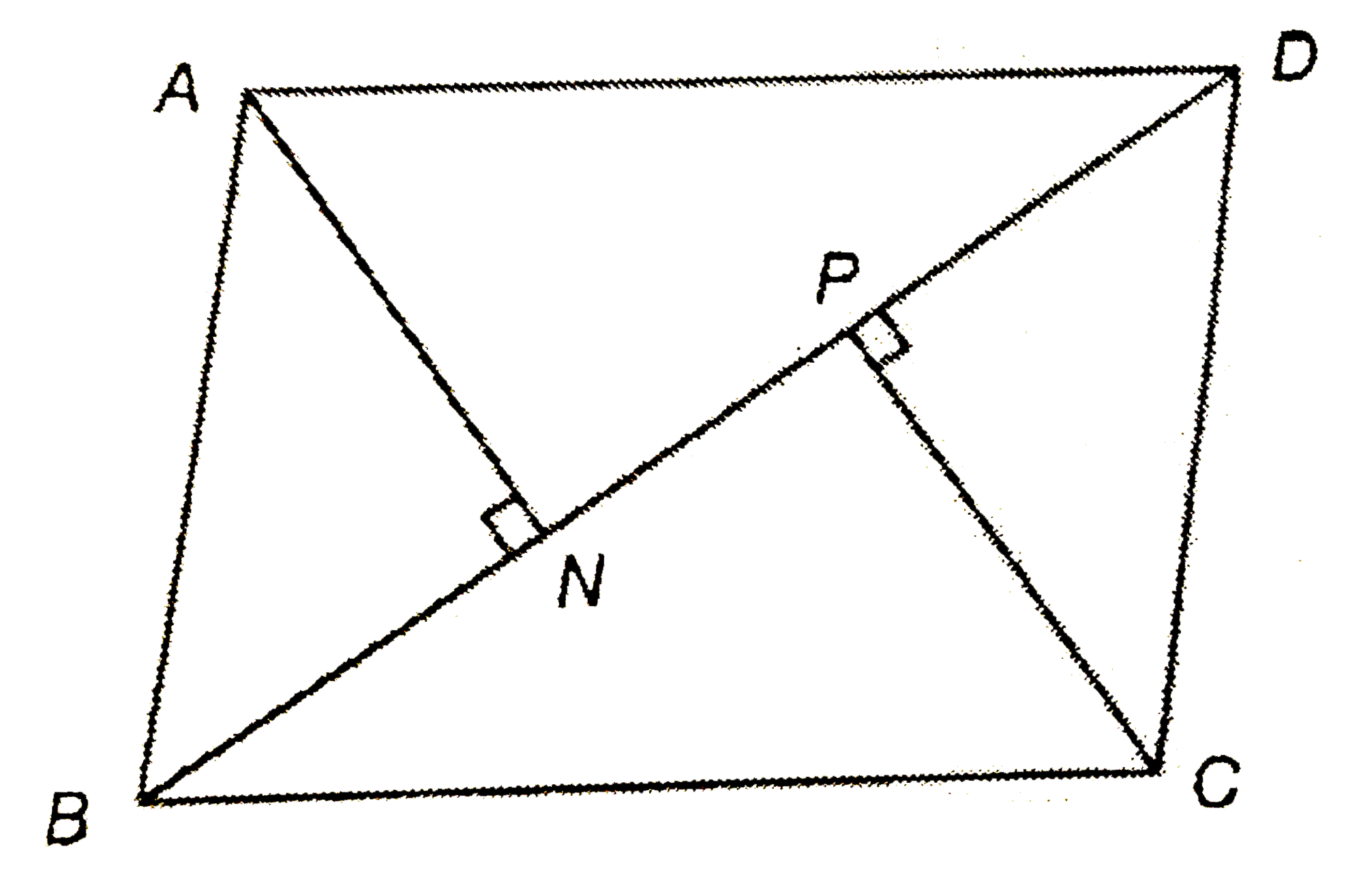
View SolutionIn the given figure, ABCD is a parallelogram in which AN and CP are perpendiculars on diagonal BD. Prove that :
(i) ΔADN=ΔCBP
(ii)AN=CP
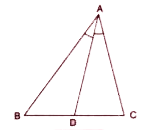
View SolutionIn the figure, given alongside, AD bisects angle BAC. Prove that :
(i) AB>BD
(ii) AC>CD
(iii) AB+AC>BC
View Solution
