Two simple pendulums A and B have equal lengths, but their bobs weigh 50 gm and 100 gm, respectively. What would be the ratio of their time periods? Give reasons for your answer.
To find the ratio of the time periods of two simple pendulums A and B, we can follow these steps:
1. Understand the Concept of Time Period:
The time period (T) of a simple pendulum is the time taken for one complete oscillation. It is given by the formula:
T=2π√Lg
where L is the length of the pendulum and g is the acceleration due to gravity.
2. Identify Given Information:
- Both pendulums A and B have equal lengths (let's denote this length as L).
- The weights of the bobs are different: pendulum A has a weight of 50 gm, and pendulum B has a weight of 100 gm.
3. Analyze the Formula:
From the formula T=2π√Lg, we see that the time period depends only on the length of the pendulum and the acceleration due to gravity. It does not depend on the mass of the bob.
4. Calculate the Time Periods:
Since both pendulums have the same length L and are subjected to the same gravitational acceleration g, we can denote the time periods of pendulums A and B as:
TA=2π√LgandTB=2π√Lg
5. Determine the Ratio of Time Periods:
Since TA and TB are equal, the ratio of their time periods can be calculated as:
TATB=2π√Lg2π√Lg=1
Therefore, the ratio of the time periods of pendulums A and B is:
Ratio=1:1
Conclusion:
The ratio of the time periods of pendulums A and B is 1:1 because the time period of a simple pendulum is independent of the mass of the bob, depending only on the length of the pendulum and the acceleration due to gravity.
The time period (T) of a simple pendulum is the time taken for one complete oscillation. It is given by the formula:
T=2π√Lg
where L is the length of the pendulum and g is the acceleration due to gravity.
- Both pendulums A and B have equal lengths (let's denote this length as L).
- The weights of the bobs are different: pendulum A has a weight of 50 gm, and pendulum B has a weight of 100 gm.
From the formula T=2π√Lg, we see that the time period depends only on the length of the pendulum and the acceleration due to gravity. It does not depend on the mass of the bob.
Since both pendulums have the same length L and are subjected to the same gravitational acceleration g, we can denote the time periods of pendulums A and B as:
TA=2π√LgandTB=2π√Lg
Since TA and TB are equal, the ratio of their time periods can be calculated as:
TATB=2π√Lg2π√Lg=1
Therefore, the ratio of the time periods of pendulums A and B is:
Ratio=1:1
The ratio of the time periods of pendulums A and B is 1:1 because the time period of a simple pendulum is independent of the mass of the bob, depending only on the length of the pendulum and the acceleration due to gravity.
Topper's Solved these Questions
- MEASUREMENTS AND EXPERIMENTATION BOOK - ICSECHAPTER - MEASUREMENTS AND EXPERIMENTATION EXERCISE - TOPIC 2 SIMPLE PENDULUM (3 Marks Questions )
10 Videos
- MEASUREMENTS AND EXPERIMENTATION BOOK - ICSECHAPTER - MEASUREMENTS AND EXPERIMENTATION EXERCISE - TOPIC 2 SIMPLE PENDULUM (4 Marks Questions )
1 Videos
- MEASUREMENTS AND EXPERIMENTATION BOOK - ICSECHAPTER - MEASUREMENTS AND EXPERIMENTATION EXERCISE - TOPIC 1 INTERNATIONAL SYSTEM OF UNITS (4 Marks Questions )
2 Videos
- MAGNETISM BOOK - ICSECHAPTER - MAGNETISM EXERCISE - EXERCISE-10(B) (Multiple Choice Type)
2 Videos
- MOTION IN ONE DIMENSION BOOK - ICSECHAPTER - MOTION IN ONE DIMENSION EXERCISE - EXERCISE -2 (C) ( Multiple choice type :)
17 Videos
Similar Questions
Can a triangle have two obtuse angles ? Give reason for your answer.
View SolutionTwo simple pendulums A and B have lengths 1.0 m and 4.0 m respectively at a certain place. Which pendulum will make more oscillations in 1 minute ? Explain your answer.
View SolutionWhich of the above two graphs : (a) and (b)the human voice is likely to be the male voice ? Give reason for your answer.
 .
.
View SolutionConsider the following circuit :
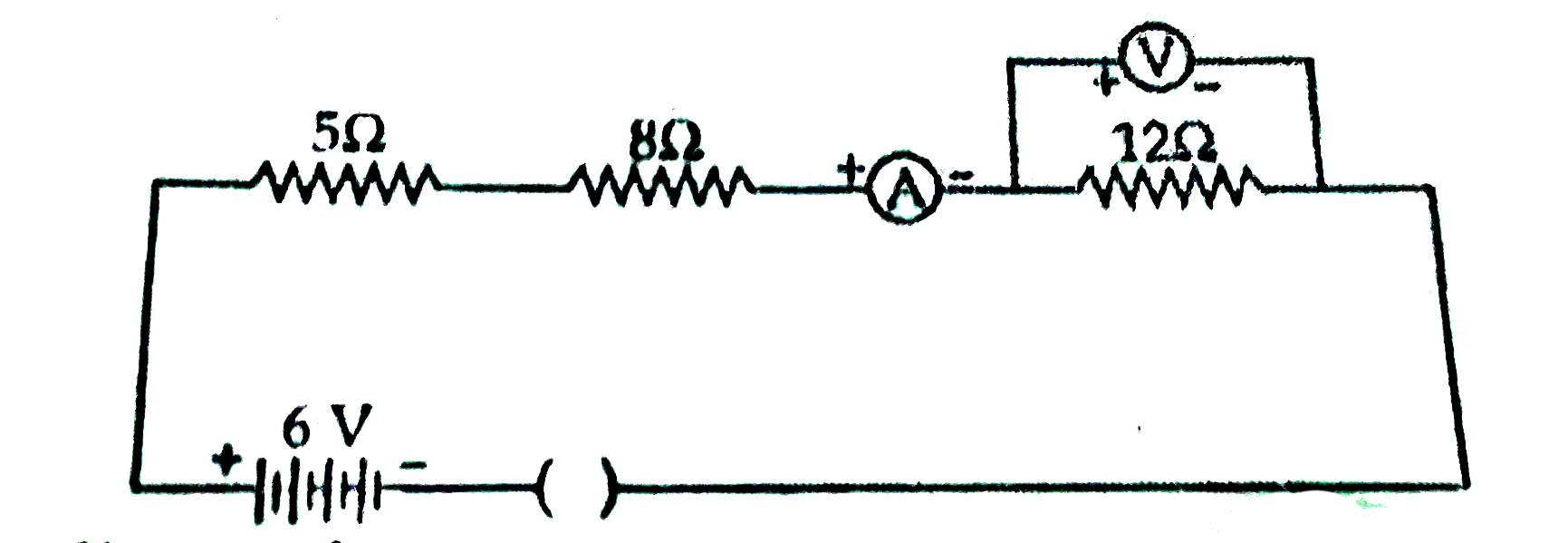
What would be the readings of the ammeter and the voltmeter when key is closed ? Give reason to justify your answers .
View SolutionTwo equal and opposite forces act on a stationary body. Will the body move ? Give reason to your answer.
View Solution
Two simple pendulums A and B having lengths l and l4 respectively are released from the position as shown in Fig. Calculate the time (in seconds) after which the two strings become parallel for the first time. (Take l=90π2m and g=10ms2.
View SolutionTwo simple pendulums of equal length cross each other at mean position. What is their phase difference ?
View SolutionIf the length of a simple pendulum is equal to the radius of the earth, its time period will be
View SolutionTwo simple pendulums have time period 4s and 5s respectively. If they started simultaneously from the mean position in the same direction, then the phase difference between them by the time the larger one completes one oscillation is
View SolutionTwo simple pendulums of length 0.5 m and 20 m, respectively are given small linear displacement in one direction at the same time. They will again be in the phase when the pendulum of shorter length has completed oscillations.
View Solution
