A solid iron ball of mass 500 g is dropped in mercury contained in a beaker.
Will the ball float or sink? Give reasons.
To determine whether the solid iron ball will float or sink in mercury, we can follow these steps:
Step 1: Understand the concept of density
Density is defined as mass per unit volume. It is a crucial factor in determining whether an object will float or sink in a fluid. An object will float if its density is less than the density of the fluid it is placed in.
Step 2: Find the density of the iron ball
The mass of the iron ball is given as 500 g. The density of iron is approximately 7.87 g/cm³.
Step 3: Find the density of mercury
The density of mercury is approximately 13.6 g/cm³.
Step 4: Compare the densities
Now, we compare the density of the iron ball with the density of mercury:
- Density of iron = 7.87 g/cm³
- Density of mercury = 13.6 g/cm³
Since the density of the iron ball (7.87 g/cm³) is less than the density of mercury (13.6 g/cm³), we can conclude that the iron ball will float.
Step 5: Explain the reason
The reason the iron ball floats is due to the principle of buoyancy. According to Archimedes' principle, an object submerged in a fluid experiences an upward force (upthrust) equal to the weight of the fluid displaced by the object. In this case, the upthrust provided by the mercury is greater than the weight of the iron ball, allowing it to float.
Conclusion
The solid iron ball will float in mercury because its density is less than that of mercury, and the buoyant force acting on it is sufficient to counteract its weight.
---
Density is defined as mass per unit volume. It is a crucial factor in determining whether an object will float or sink in a fluid. An object will float if its density is less than the density of the fluid it is placed in.
The mass of the iron ball is given as 500 g. The density of iron is approximately 7.87 g/cm³.
The density of mercury is approximately 13.6 g/cm³.
Now, we compare the density of the iron ball with the density of mercury:
- Density of iron = 7.87 g/cm³
- Density of mercury = 13.6 g/cm³
The reason the iron ball floats is due to the principle of buoyancy. According to Archimedes' principle, an object submerged in a fluid experiences an upward force (upthrust) equal to the weight of the fluid displaced by the object. In this case, the upthrust provided by the mercury is greater than the weight of the iron ball, allowing it to float.
The solid iron ball will float in mercury because its density is less than that of mercury, and the buoyant force acting on it is sufficient to counteract its weight.
Topper's Solved these Questions
- FLUIDSBOOK - ICSECHAPTER - FLUIDSEXERCISE - TOPIC 2 (3 Marks Questions )
23 Videos
- FLUIDSBOOK - ICSECHAPTER - FLUIDSEXERCISE - TOPIC 2 (4 Marks Questions )
16 Videos
- FLUIDSBOOK - ICSECHAPTER - FLUIDSEXERCISE - TOPIC 1 (4 Marks Questions )
10 Videos
- ELECTRICITY AND MAGNETISM BOOK - ICSECHAPTER - ELECTRICITY AND MAGNETISM EXERCISE - TOPIC 2 Magnetism (4 Marks Questions )
6 Videos
- HEAT AND ENERGYBOOK - ICSECHAPTER - HEAT AND ENERGYEXERCISE - EXERCISE -6(D) Multiple Choice Question)
4 Videos
Similar Questions
A solid iron ball of mass 500 g is dropped in mercury contained in a beaker.
What will be the apparent weight of the ball?
View SolutionYou are provided with a hollow iron ball A of volume 15cm3 and mass 12 g and a solid iron ball B of mass 12 g. Both are placed on the surface of water contained in a large tub.
Which ball will sink? Give a reason for your answer. (Density of iron = 8.0g cm−3)
View SolutionYou are provided with a hollow iron ball A of volume 5cm3 and mass 12 g and a solid iron ball B of mass 12 g. Both are plced on the surface of water contained in a largetub. A. Find upthrust on each ball. B. Which ball will sink? Give reason for your answer. (Density of iron =8.0gm−3)
View SolutionYou are provided with a hollow iron ball A of volume 15cm3 and mass 12 g and a solid iron ball B of mass 12 g. Both are placed on the surface of water contained in a large tub.
Find upthrust on each ball.
View SolutionA cylindrical beaker, whose base has a radius of 15 cm, is filled with water up to a height of 20 cm. A heavy iron spherical ball of radius 10 cm is dropped to submerge completely in water in the beaker. Find the increase in the level of water.
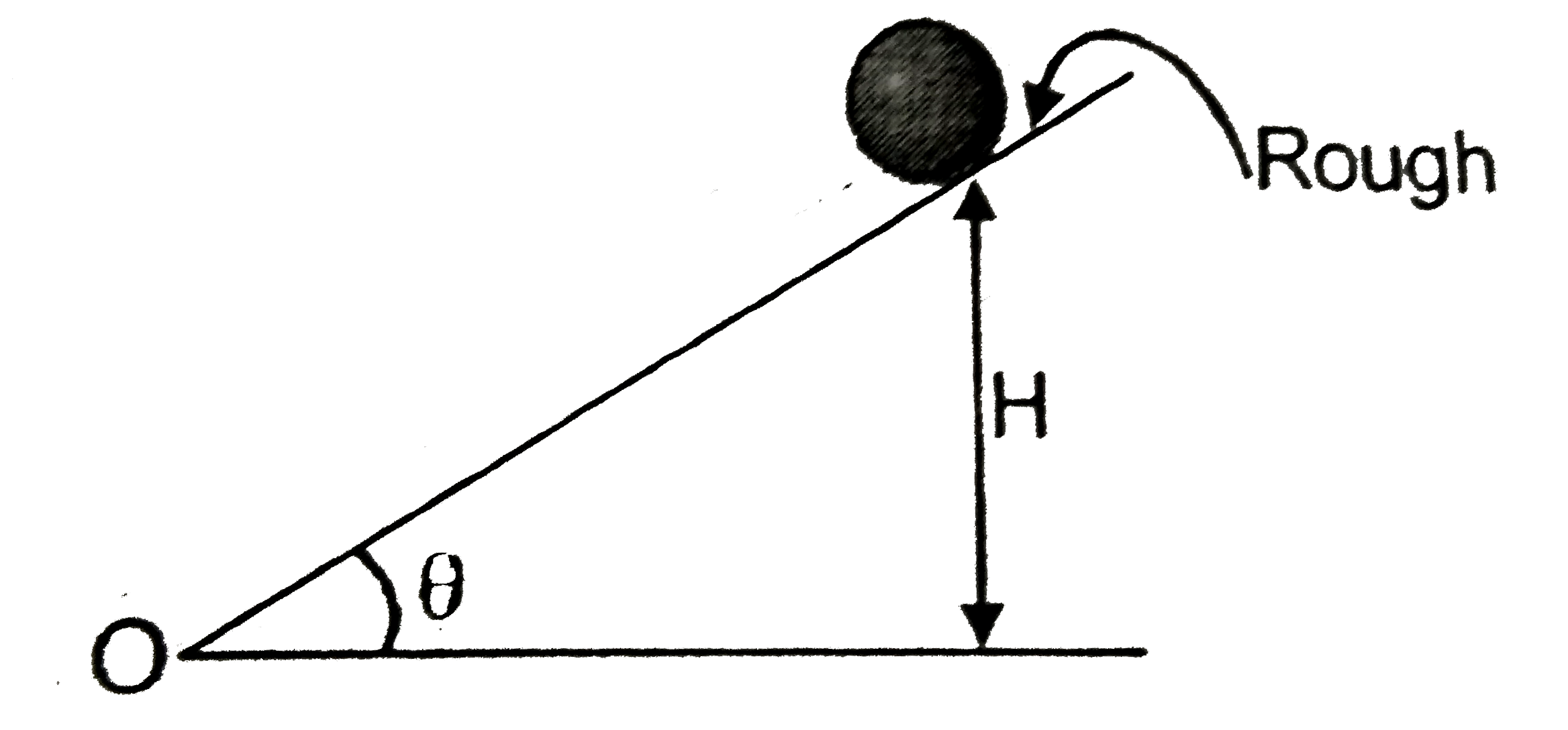
View SolutionA solid ball of mass 'm' is released on a rough fixed inclined plane from height H. The ball will perform pure rolling on the inclined plane. Then
View SolutionA cube of iron of edge 5cm floats on the surface of mercury, contained in a tank. Water is then poured on top, so that the cube just gets immersed. Find the depth of water layer. (Specific gravities of iron-and mercury are 7.8 and 13.6, respectively.)
View SolutionA ball floats on the surface of water in a container exposed to the atmosphere. Will the ball remain immersed at its initial depth or will it sink or rise somewhat if the container is shifted to the moon?
View SolutionExplain why an iron nail floats on mercury, but it sinks in water.
View SolutionA cylinder of radius 12cm contains water to a depth of 20cm. A spherical iron ball is dropped into the cylinder and thus the level of water is raised by 6.75 cm. Find the radius of the ball. (use π=227)
View Solution
