Find out the units and dimensions of the constants a and b in the vander waal.s equation (P+aV2)(V−b)=RT.
To find the units and dimensions of the constants a and b in the Van der Waals equation
(P+aV2)(V−b)=RT,
we will analyze the equation step by step.
Step 1: Understand the equation
The Van der Waals equation relates pressure P, volume V, temperature T, and constants a and b. Here, R is the universal gas constant.
Step 2: Identify the dimensions of pressure P
Pressure P is defined as force per unit area. The dimensions of force are given by:
Force=mass×acceleration=M⋅L⋅T−2.
Area has dimensions of L2. Therefore, the dimensions of pressure P are:
(P)=M⋅L⋅T−2L2=M⋅L−1⋅T−2.
Step 3: Analyze the term aV2
For the term aV2 to have the same dimensions as pressure P, we need to find the dimensions of V first. The volume V has dimensions L3. Therefore, the dimensions of V2 are:
(V2)=(L3)2=L6.
Now, we can express the dimensions of a:
(aV2)=(P)⟹(a)=(P)⋅(V2)=(M⋅L−1⋅T−2)⋅(L6)=M⋅L5⋅T−2.
Step 4: Find the dimensions of constant b
The term V−b must also have the same dimensions as V. Thus, the dimensions of b must be the same as the dimensions of volume V:
(b)=(V)=L3.
Final Results
Thus, the dimensions of the constants a and b are:
- Dimensions of a: M1L5T−2
- Dimensions of b: L3
- Dimensions of b: L3
Topper's Solved these Questions
- BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER-3 EXERCISE - SECTION-D6videos
SAMPLE QUESTION PAPER-3
- BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER-3 EXERCISE - SECTION-B14videos
SAMPLE QUESTION PAPER-3
- BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER-2 EXERCISE - SECTION-D10videos
SAMPLE QUESTION PAPER-2
- BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 01EXERCISE - SECION- D (Answer the following )6videos
SELF ASSESSMENT PAPER 01
Similar Questions
Knowledge Check
- Question 1 - Select One
In the Van der Waals equation (P+aV2)(V−b) = constant, the unit of a is
Adyne/cm5Bdyne/cm4Cdyne/cm3Ddyne/cm2 - Question 2 - Select One
The van der Waal equation of gas is
(P+n2aV2)(V−nb)=nRTA(i) CO2 , (ii) H2B(i) CH4 , (ii) CO2C(i) H2 , (ii) CO2DO2, (ii) H2
The units of constant b used in van der Waals' equation are ………….. .
View SolutionWrite the units of van der Waals' constant 'a' and 'b'.
View SolutionThe ratio of units of van der Waals constants a and b is
View SolutionFor real gases, the relation between P, V and T is given by an van der Waals equation, (P+an2V2)(V−nb)=nRT.
For the following gases CH4,CO2,O2,H2 which gas will have (i) highest value of 'a' and (ii) lowest value of 'b' respectively?View SolutionThe ratio a/b (the terms used in van der Waals' equation) has the unit .
View SolutionAt a particular temperature and pressure for a real gas Van der Waal's equation can be written as:
(P+aV2m)(Vm−b)=RT
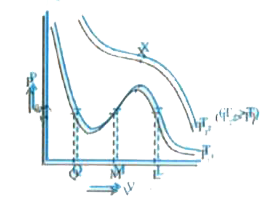
where Vm is molar volume of gas. This is cubic equation in the variable Vm and therefore for any single value of P & T there should be 3 values of Vm. Which are shown in graph as Q, M and L.
As temperature is made to increase at a certain higher temperature the three values of Vm becomes identical. The temperature, pressure & molar volume at point X are called Tc, Pc & Vc for real gas. The compressibility factor in terms of Pc, Vc and T is called Zc.
The expression of Van dcr Waal's constant 'a' can be given asView Solution

