Which two of the following five physical parameters have the same dimension?
(1) Energy density
(2) refractive index
(3) dielectric constant
(4) Young's modulus
(5) magnitic field
(ii) and (iv)
(iii) and (v)
(i) and (iv)
(i) and (v)
The correct Answer is:C
To determine which two of the five physical parameters have the same dimension, we will analyze each parameter one by one.
1. Energy Density (U):
- Energy density is defined as energy per unit volume.
- The dimension of energy (E) is given by (E)=ML2T−2.
- Therefore, the dimension of energy density is:
(U)=(E)(L3)=ML2T−2L3=ML−1T−2
2. Refractive Index (n):
- The refractive index is defined as the ratio of the speed of light in vacuum to the speed of light in a medium.
- It is a dimensionless quantity, so:
(n)=1
3. Dielectric Constant (ε):
- The dielectric constant is also defined as the ratio of the capacitance of a capacitor with a dielectric to the capacitance without it.
- Like the refractive index, it is dimensionless, so:
(ε)=1
4. Young's Modulus (Y):
- Young's modulus is defined as the ratio of stress to strain.
- The dimension of stress (force per unit area) is:
(Stress)=(F)(A)=MLT−2L2=ML−1T−2
- Strain is dimensionless, so:
(Y)=(Stress)(Strain)=ML−1T−2
5. Magnetic Field (B):
- The magnetic field can be defined in terms of force per unit charge per unit velocity.
- The dimension of the magnetic field is:
(B)=(F)(q)(v)=MLT−2IT=MA−1T−2
Now, we summarize the dimensions:
- Energy Density: ML−1T−2
- Refractive Index: 1 (dimensionless)
- Dielectric Constant: 1 (dimensionless)
- Young's Modulus: ML−1T−2
- Magnetic Field: MA−1T−2
From the above analysis, we can see that:
- Energy Density and Young's Modulus both have the dimension ML−1T−2.
Thus, the two parameters with the same dimension are:
Energy Density (1) and Young's Modulus (4).
Final Answer:
The two parameters with the same dimension are (1) Energy Density and (4) Young's Modulus.
---
- Energy density is defined as energy per unit volume.
- The dimension of energy (E) is given by (E)=ML2T−2.
- Therefore, the dimension of energy density is:
(U)=(E)(L3)=ML2T−2L3=ML−1T−2
- The refractive index is defined as the ratio of the speed of light in vacuum to the speed of light in a medium.
- It is a dimensionless quantity, so:
(n)=1
- The dielectric constant is also defined as the ratio of the capacitance of a capacitor with a dielectric to the capacitance without it.
- Like the refractive index, it is dimensionless, so:
(ε)=1
- Young's modulus is defined as the ratio of stress to strain.
- The dimension of stress (force per unit area) is:
(Stress)=(F)(A)=MLT−2L2=ML−1T−2
- Strain is dimensionless, so:
(Y)=(Stress)(Strain)=ML−1T−2
- The magnetic field can be defined in terms of force per unit charge per unit velocity.
- The dimension of the magnetic field is:
(B)=(F)(q)(v)=MLT−2IT=MA−1T−2
- Energy Density: ML−1T−2
- Refractive Index: 1 (dimensionless)
- Dielectric Constant: 1 (dimensionless)
- Young's Modulus: ML−1T−2
- Magnetic Field: MA−1T−2
- Energy Density and Young's Modulus both have the dimension ML−1T−2.
Energy Density (1) and Young's Modulus (4).
The two parameters with the same dimension are (1) Energy Density and (4) Young's Modulus.
Similar Questions
Which physical quantities have the same dimensions of ML−1T−2?
View SolutionWhich of the following pairs have same dimensional formula for both the quantities ?
(i) kinetic energy and torque
(ii) resistance and inductance
(iii) Young's Modulus and Pressure
View SolutionA convex lens L1 and a concave lens L2 have refractive index 32. Match the following two columns.

View SolutionIn the diagram shown, light is incident on the interface between media 1 (refractive index n1) and 2 (refractive index n2) at angle slightly greater than the critical angle, and is totally reflected. The light is then also totally reflected at the interface between media 1 and 3 (refractive index n3), after which it travels in a direction opposite to its initial direction, The media must have a refractive indices such that.
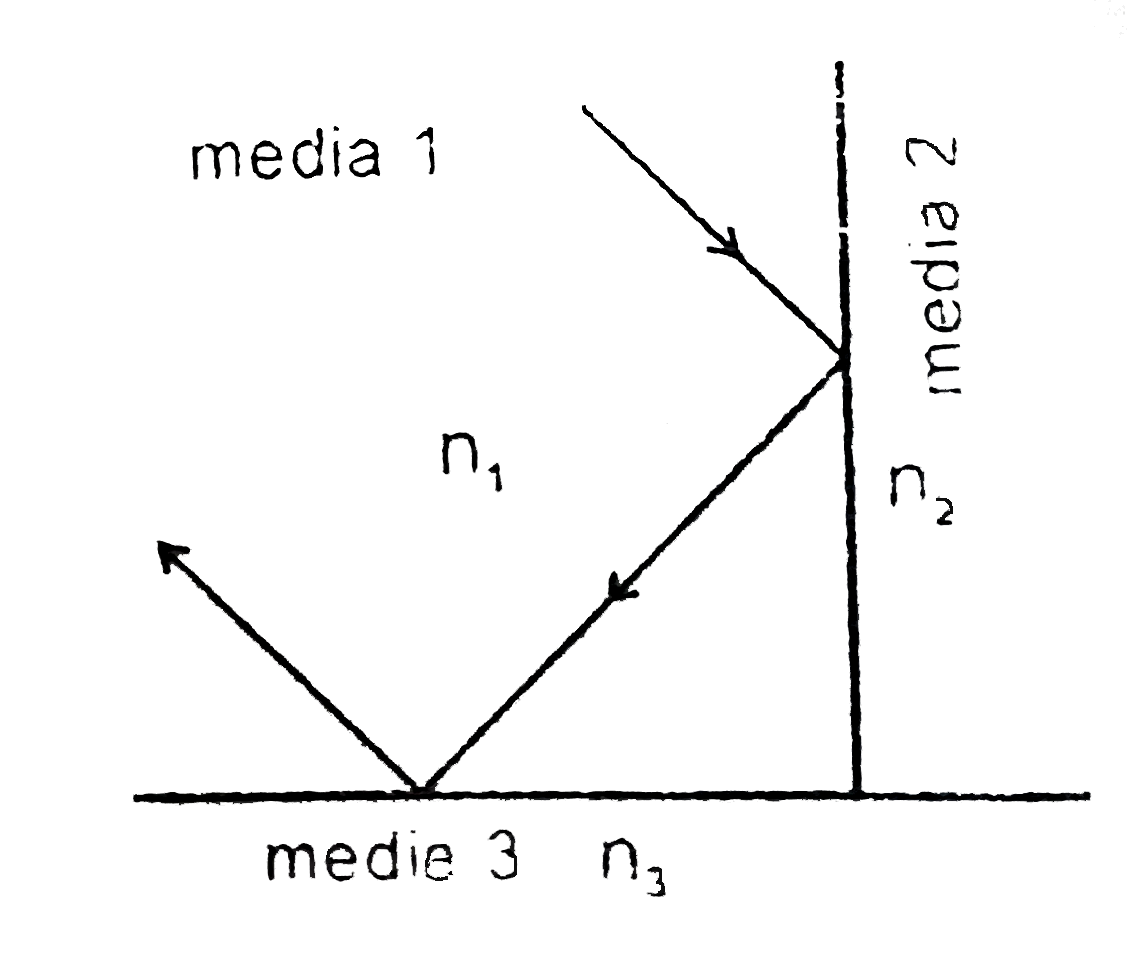 .
.
View SolutionIn Young's double slit experiment, the fringes are displaced index 1.5 is introduced in the path of one of the beams. When this plate in replaced by another plate of the same thickness, the shift of fringes is (3/2)x. The refractive index of the second plate is
View SolutionA parallel plate capacitor of area A, plate separation d and capacitance C is filled with four dielectric materials hving dielectric constants K1,K2,K3 and K4 as shown in the figure below. If a single dielectric material is to be used to have the same capacitance c in this capacitor, then its dielectric constant K is given by

View SolutionA wire having a length 1 m and cross-section area 3mm2 is suspended at one of its ends from a ceiling. What will be its strain energy due to its own weight, if the density and Young's modulus of the material of the wire be 10g/cm3 and 1.2×1011N/m2 respectively.
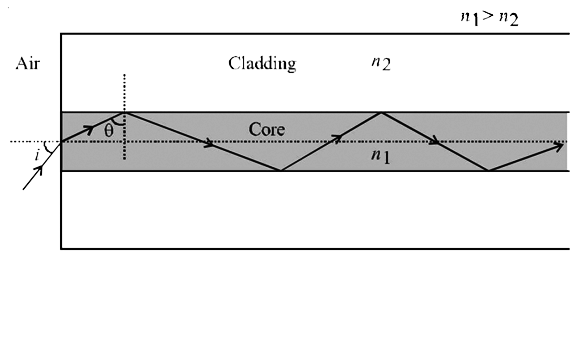
View SolutionLight guidance in an optical fibre can be understood by considering a structure comprising of thin solid glass cylinder of refractive index n1 surrounded by a medium of lower refractive index n2. The light guidance in the structure takes place due to successive total internal reflectrions at the interface of the media n1 and n2 as shown in the fugure. All rays with the angle of incidence i less than a particular value im are confined in the medium of refractive index n1. The numerical aprture (NA) of the structure is defined as sinim
For two structure namely S1 with n1=√454 and n2=32, and S2 with n1=85 and n2=75 and taking the refractive index of water to be 43 and that of air to be 1, the correct option (s) is (are) ?
View SolutionTwo light waves having the same wavelength λ in vacuum are in phase initially. Then the first ray travels a path of length L1 through a medium of refractive index μ1. Then second ray travels a path of length L2 throug a medium of refractive index μ2. The two waves are then combined to observed interference effects. The phase difference between the two, when they interfere, is
View SolutionTwo light waves having the same wavelength λ in vacuum are in phase initially. Then the first ray travels a path of length L1 through a medium of refractive index μ1. Then second ray travels a path of length L2 throug a medium of refractive index μ2. The two waves are then combined to observed interference effects. The phase difference between the two, when they interfere, is
View Solution