Two persons of masses 55kg and 65kg respectively are at the opposite ends of a boat. The length of the boat is 3.0m and weights 100kg. The 55kg man walks up to the 65kg man and sits with him. If the boat is in still water the centre of mass of the system shifts by.
3m
2.3m
zero
0.75m
The correct Answer is:c
To solve the problem, we need to analyze the system consisting of two persons and a boat. We will calculate the center of mass before and after the 55 kg person moves towards the 65 kg person.
1. Identify the System:
- We have two persons with masses m1=55kg and m2=65kg.
- The mass of the boat is mb=100kg.
- The length of the boat is L=3.0m.
2. Determine Initial Positions:
- Let’s assume the left end of the boat is at position x=0 m and the right end is at position x=3.0 m.
- The 55 kg person is at the left end (position x1=0 m).
- The 65 kg person is at the right end (position x2=3.0 m).
- The center of mass of the boat is at its midpoint, which is xb=1.5 m.
3. Calculate Initial Center of Mass:
- The total mass of the system M=m1+m2+mb=55+65+100=220kg.
- The initial center of mass xcm,initial can be calculated using the formula:
xcm,initial=m1x1+m2x2+mbxbM
Substituting in the values:
xcm,initial=(55×0)+(65×3)+(100×1.5)220=0+195+150220=345220≈1.568m
4. Determine Final Positions:
- When the 55 kg person walks to the 65 kg person, they both will be at the same position, which is at the right end of the boat (position x=3.0 m).
- The center of mass of the boat remains at xb=1.5 m.
5. Calculate Final Center of Mass:
- The final center of mass xcm,final can be calculated as:
xcm,final=m1xf+m2xf+mbxbM
where xf=3.0 m (the position where both persons are sitting).
xcm,final=(55×3)+(65×3)+(100×1.5)220=165+195+150220=510220≈2.318m
6. Calculate the Shift in Center of Mass:
- The shift in the center of mass Δxcm is given by:
Δxcm=xcm,final−xcm,initial=2.318−1.568≈0.75m
Conclusion:
The center of mass of the system shifts by approximately 0.75m.
- We have two persons with masses m1=55kg and m2=65kg.
- The mass of the boat is mb=100kg.
- The length of the boat is L=3.0m.
- Let’s assume the left end of the boat is at position x=0 m and the right end is at position x=3.0 m.
- The 55 kg person is at the left end (position x1=0 m).
- The 65 kg person is at the right end (position x2=3.0 m).
- The center of mass of the boat is at its midpoint, which is xb=1.5 m.
- The total mass of the system M=m1+m2+mb=55+65+100=220kg.
- The initial center of mass xcm,initial can be calculated using the formula:
xcm,initial=m1x1+m2x2+mbxbM
Substituting in the values:
xcm,initial=(55×0)+(65×3)+(100×1.5)220=0+195+150220=345220≈1.568m
- When the 55 kg person walks to the 65 kg person, they both will be at the same position, which is at the right end of the boat (position x=3.0 m).
- The center of mass of the boat remains at xb=1.5 m.
- The final center of mass xcm,final can be calculated as:
xcm,final=m1xf+m2xf+mbxbM
where xf=3.0 m (the position where both persons are sitting).
xcm,final=(55×3)+(65×3)+(100×1.5)220=165+195+150220=510220≈2.318m
- The shift in the center of mass Δxcm is given by:
Δxcm=xcm,final−xcm,initial=2.318−1.568≈0.75m
The center of mass of the system shifts by approximately 0.75m.
Similar Questions
Two particles of masses 1kg and 2kg are located at x=0 and x=3m. Find the position of their centre of mass.
View SolutionTwo particles of masses 1kg and 2kg are located at x=0 and x=3m. Find the position of their centre of mass.
View SolutionTwo persons A and B of weight 80kg and 50kg respectively are standing at opposite ends of a boat of mass 70kg and length 2m at rest. When they interchange their positions then displacement of the centre of mass of the boat will be :-

View SolutionTwo particles of mass 5 kg and 10 kg respectively are attached to the twoends of a rigid rod of length 1 m with negligible mass. the centre of mass of the system from the 5 kg particle is nearly at a distance of :
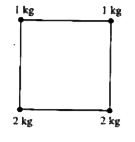
View SolutionFour point masses 1 kg, 1 kg, 2 kg and 2 kg are placed at the corners of a square of side a m as shown in Fig. Find the centre of mass of the system.
View SolutionTwo bodies of masses 0.5 kg and 1 kg are lying in the X-Y plane at points (-1, 2) and (3, 4) respectively. Locate the centre of mass of the system.
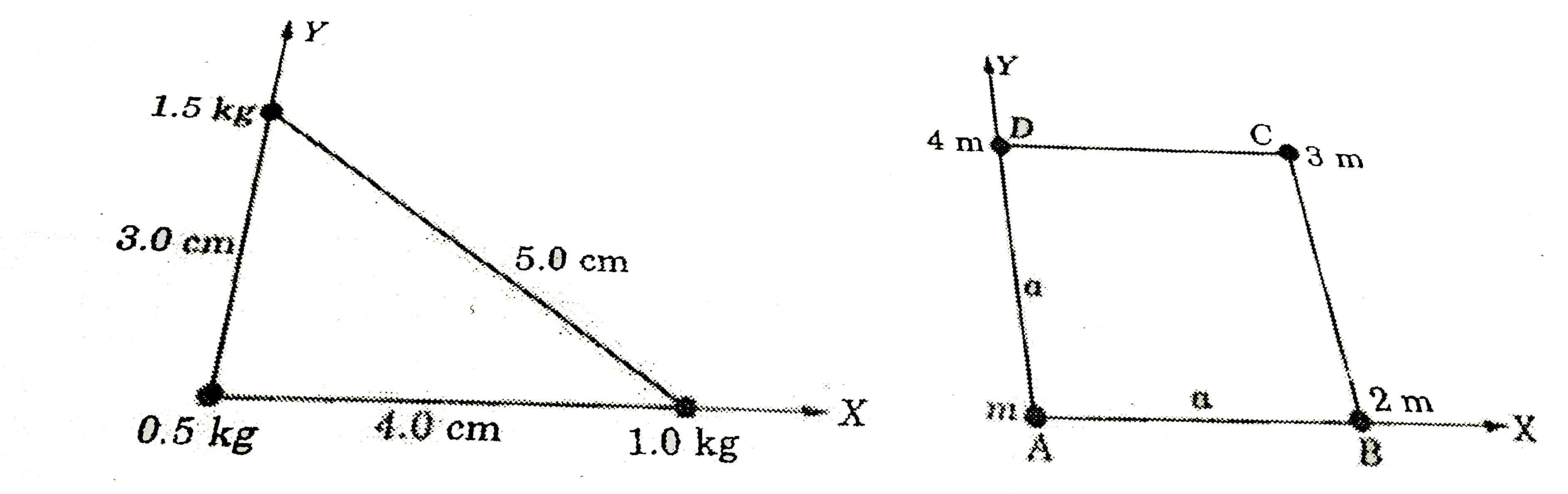
View SolutionThree particles of masses 0.50 kg, 1.0 kg and are placed at the corners of a right angle triangle, as shown in fig. Locate the centre of mass of the system.
View SolutionA person of mass 70 kg jump from a 3.0m height
View SolutionTwo point masses of 3.0 kg and 1.0 kg are attached to opposite ends of a horizontal spring whose spring constant is 300Nm−1 as shown in the figure. The natural vibration frequency of the system is of the order of :

View SolutionTwo bodies of masses 1 kg and 3 kg are lying in xy plane at (0, 0) and (2, -1) respectively. What are the coordinates of the centre of mass ?
View Solution
