A person of mass 70 kg jump from a 3.0m height
Impulse on the main by ground will be 539N−s
average force on man if the landing is with stiffed leg and body moves by 1.0cm during impact is 2.1×105N
average force on man feet by ground if he land with bent legs and body moves by 50cm is 4.2×103N
average force on man feet by ground if he land with bent legs and body moves by 50cm is (4.9×103N)
The correct Answer is:A, B, D
To solve the problem of a person with a mass of 70 kg jumping from a height of 3.0 m, we will follow these steps:
Step 1: Calculate the final velocity just before hitting the ground
Using the equation of motion:
v2=u2+2gh
where:
- v = final velocity just before impact,
- u = initial velocity (0 m/s, since the person jumps from rest),
- g = acceleration due to gravity (approximately 10m/s2),
- h = height (3.0 m).
Substituting the values:
v2=0+2×10×3
v2=60
v=√60≈7.75m/s
Step 2: Calculate the impulse on the person by the ground
Impulse is given by the change in momentum:
Impulse=Δp=m(v−0)
where:
- m=70kg,
- v≈7.75m/s.
Calculating the impulse:
Impulse=70×7.75≈542.5Ns
Step 3: Calculate the average force during the impact
The average force can be calculated using the work-energy principle:
Faverage⋅d=ΔKE
where:
- d = distance over which the force acts (let's consider two cases: 1 cm and 50 cm),
- ΔKE=12mv2.
Calculating the change in kinetic energy:
ΔKE=12×70×(7.75)2
ΔKE=12×70×60≈2100J
Case 1: For d=0.01m (1 cm)
Using the formula:
Faverage=ΔKEd
Faverage=21000.01=210000N
Case 2: For d=0.50m (50 cm)
Faverage=21000.50=4200N
Summary of Results
1. Final velocity just before impact: ≈7.75m/s
2. Impulse on the person by the ground: ≈542.5Ns
3. Average force during impact:
- For 1 cm: 210000N
- For 50 cm: 4200N
Using the equation of motion:
v2=u2+2gh
where:
- v = final velocity just before impact,
- u = initial velocity (0 m/s, since the person jumps from rest),
- g = acceleration due to gravity (approximately 10m/s2),
- h = height (3.0 m).
v2=0+2×10×3
v2=60
v=√60≈7.75m/s
Impulse is given by the change in momentum:
Impulse=Δp=m(v−0)
where:
- m=70kg,
- v≈7.75m/s.
Impulse=70×7.75≈542.5Ns
The average force can be calculated using the work-energy principle:
Faverage⋅d=ΔKE
where:
- d = distance over which the force acts (let's consider two cases: 1 cm and 50 cm),
- ΔKE=12mv2.
ΔKE=12×70×(7.75)2
ΔKE=12×70×60≈2100J
Using the formula:
Faverage=ΔKEd
Faverage=21000.01=210000N
Faverage=21000.50=4200N
1. Final velocity just before impact: ≈7.75m/s
2. Impulse on the person by the ground: ≈542.5Ns
3. Average force during impact:
- For 1 cm: 210000N
- For 50 cm: 4200N
Similar Questions
A person of mass 70kg jumps from a stationary helicopter with the parachute open. As he falls through 50m height, he gains a speed of 20ms−1. The work done by the viscous air drag is
View SolutionA body A of mass 4 kg is dropped from a height of 100 m. Another body B of mass 2 kg is dropped from a height of 50 m at the same time. Then :
View SolutionA body of mass 0.2 kg falls from a height of 10 m to a height of 6 m above the ground. Find the loss in potential energy taking place in the body.
[g=10ms−2]
View SolutionA body of mass 2kg is projected upward from the surface of the ground at t=0 with a velocity of 20m/s. One second later a body B, also of mass 2kg, is dropped from a height of 20m. If they collide elastically, then velocities just after collision are :-
View SolutionA ball of mass 1 kg is dropped from 20 m height on ground and it rebounds to height 5m. Find magnitude of change in momentum during its collision with the ground. (Take g=10m/s2)
View SolutionIn the shown figure, the heavu block of mass 2kg rests on the horizontal surface and the lighter block of mass 1kg is dropped from a height of 0.9m. At the instant the string gets taut, find the upwards speed (in m/s ) of the heavy block.
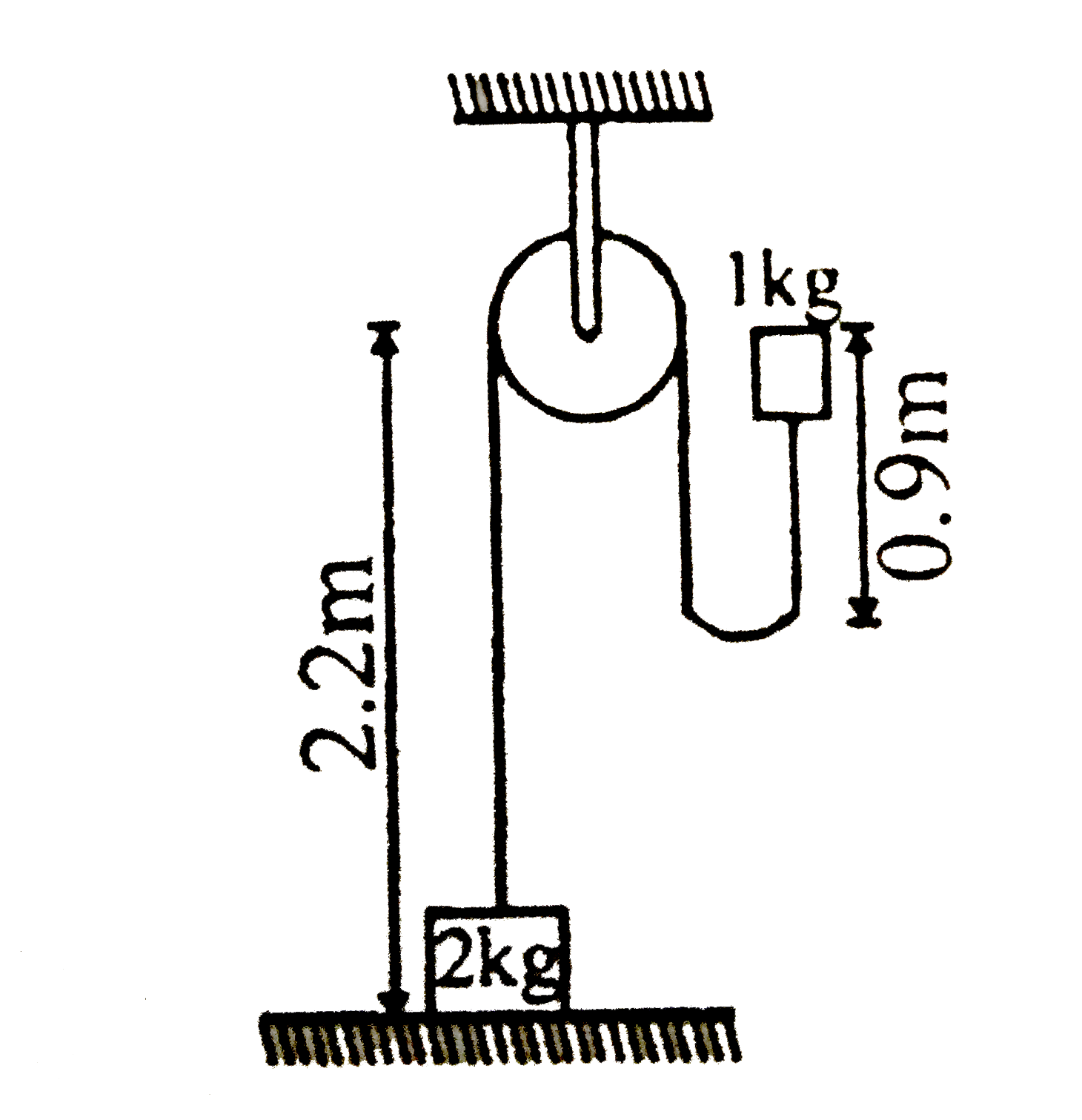
View SolutionA man of mass 60kg jumps from a trolley of mass 20kg standing on smooth surface with absolute velocity 3m/s. Find velocity of trolley and total energy produced by man.
View SolutionA bullet of mass 2g travelling at a speed of 500m/s is fired into a ballistic pendulum of mass 1.0kg suspended from a cord 1.0m long. The bullet penetrates the pendulum and emerges with a velocity of 100m/s. Through what vertical height will the pendulum rise?
View SolutionA particle of mass 1 kg is projected upwards with velocity 60 m/s. Another particle of mass 2 kg is just deopper from a certain height. After 2 kg is just of the particles have colliided with ground, match the following [ Take g= 10 m/s2]
View SolutionThe mass of a uniform ladder of length 5 m is 20 kg. A person of mass 60 kg stands on the ladder at a height of 2 m from the bottom. The position of centre of mass of the ladder and man from the bottom nearly is
View Solution
