The following four wires are made of same material. Which of these will have the largest extension when the same tension is applied?
Length =50cm, diameter =0.5mm
Length =100cm, diameter =1mm
Length =200cm, diameter =2mm
Length =300cm, diameter =3mm
The correct Answer is:a
To determine which of the four wires made of the same material will have the largest extension when the same tension is applied, we can use the formula for extension derived from Young's modulus.
1. Understand the Formula for Extension:
The extension (ΔL) of a wire under tension can be expressed as:
ΔL=FLAY
where:
- F = applied force (tension)
- L = original length of the wire
- A = cross-sectional area of the wire
- Y = Young's modulus of the material
2. Recognize Constants:
Since all wires are made of the same material, Young's modulus Y is constant for all wires. If the same tension F is applied, it is also constant.
3. Identify the Relationship:
The extension ΔL is directly proportional to the length L of the wire and inversely proportional to the cross-sectional area A:
ΔL∝LA
4. Calculate the Cross-Sectional Area:
The cross-sectional area A of a wire with diameter d is given by:
A=πd24
Therefore, as the diameter increases, the area increases, leading to a decrease in extension.
5. Evaluate Each Wire:
For each wire, calculate the ratio LA:
- Let’s denote the lengths and diameters of the wires as follows:
- Wire 1: Length = 50 cm, Diameter = 0.5 mm
- Wire 2: Length = 50 cm, Diameter = 1 mm
- Wire 3: Length = 100 cm, Diameter = 1 mm
- Wire 4: Length = 150 cm, Diameter = 1.5 mm
6. Calculate the Ratios:
- For Wire 1:
- L=50 cm, A=π(0.05)24=0.0019635 cm²
- Ratio = 500.0019635≈25400
- For Wire 2:
- L=50 cm, A=π(0.1)24=0.007854 cm²
- Ratio = 500.007854≈6366.2
- For Wire 3:
- L=100 cm, A=π(0.1)24=0.007854 cm²
- Ratio = 1000.007854≈12732.4
- For Wire 4:
- L=150 cm, A=π(0.15)24=0.017671 cm²
- Ratio = 1500.017671≈8485.3
7. Compare Ratios:
The wire with the largest ratio LA will have the largest extension. From our calculations:
- Wire 1: 25400
- Wire 2: 6366.2
- Wire 3: 12732.4
- Wire 4: 8485.3
Therefore, Wire 1 has the largest extension.
8. Conclusion:
The wire with the largest extension when the same tension is applied is Wire 1.
The extension (ΔL) of a wire under tension can be expressed as:
ΔL=FLAY
where:
- F = applied force (tension)
- L = original length of the wire
- A = cross-sectional area of the wire
- Y = Young's modulus of the material
Since all wires are made of the same material, Young's modulus Y is constant for all wires. If the same tension F is applied, it is also constant.
The extension ΔL is directly proportional to the length L of the wire and inversely proportional to the cross-sectional area A:
ΔL∝LA
The cross-sectional area A of a wire with diameter d is given by:
A=πd24
Therefore, as the diameter increases, the area increases, leading to a decrease in extension.
For each wire, calculate the ratio LA:
- Let’s denote the lengths and diameters of the wires as follows:
- Wire 1: Length = 50 cm, Diameter = 0.5 mm
- Wire 2: Length = 50 cm, Diameter = 1 mm
- Wire 3: Length = 100 cm, Diameter = 1 mm
- Wire 4: Length = 150 cm, Diameter = 1.5 mm
- For Wire 1:
- L=50 cm, A=π(0.05)24=0.0019635 cm²
- Ratio = 500.0019635≈25400
- For Wire 2:
- L=50 cm, A=π(0.1)24=0.007854 cm²
- Ratio = 500.007854≈6366.2
- For Wire 3:
- L=100 cm, A=π(0.1)24=0.007854 cm²
- Ratio = 1000.007854≈12732.4
- For Wire 4:
- L=150 cm, A=π(0.15)24=0.017671 cm²
- Ratio = 1500.017671≈8485.3
The wire with the largest ratio LA will have the largest extension. From our calculations:
- Wire 1: 25400
- Wire 2: 6366.2
- Wire 3: 12732.4
- Wire 4: 8485.3
The wire with the largest extension when the same tension is applied is Wire 1.
Similar Questions
Force constant and surface tension have the same dimensions in
View SolutionThe lengths of two wires of same material are in the ratio 1:2, their tensions are in the ratio 1:2 and their diameters are in the ratio 1:3. the ratio of the notes they emits when sounded together by the same source is
View Solution
Knowledge Check
- Question 1 - Select One
The following four wires are made of the same material which of these will have the largest extension when the same tension is applied
AÂ L=100 cm, r- 0.2 mmBÂ L=200 cm, r 0.4 mmCÂ L 300 cm, r 0.6 mmDL 400 cm, r 0.8 mm
Four wires made of same material have different lengths and radii, the wire having more resistance in the following case is
View SolutionThe load versus extension graph for four wires of same material is shown.
The thinnest wire is represented by the line
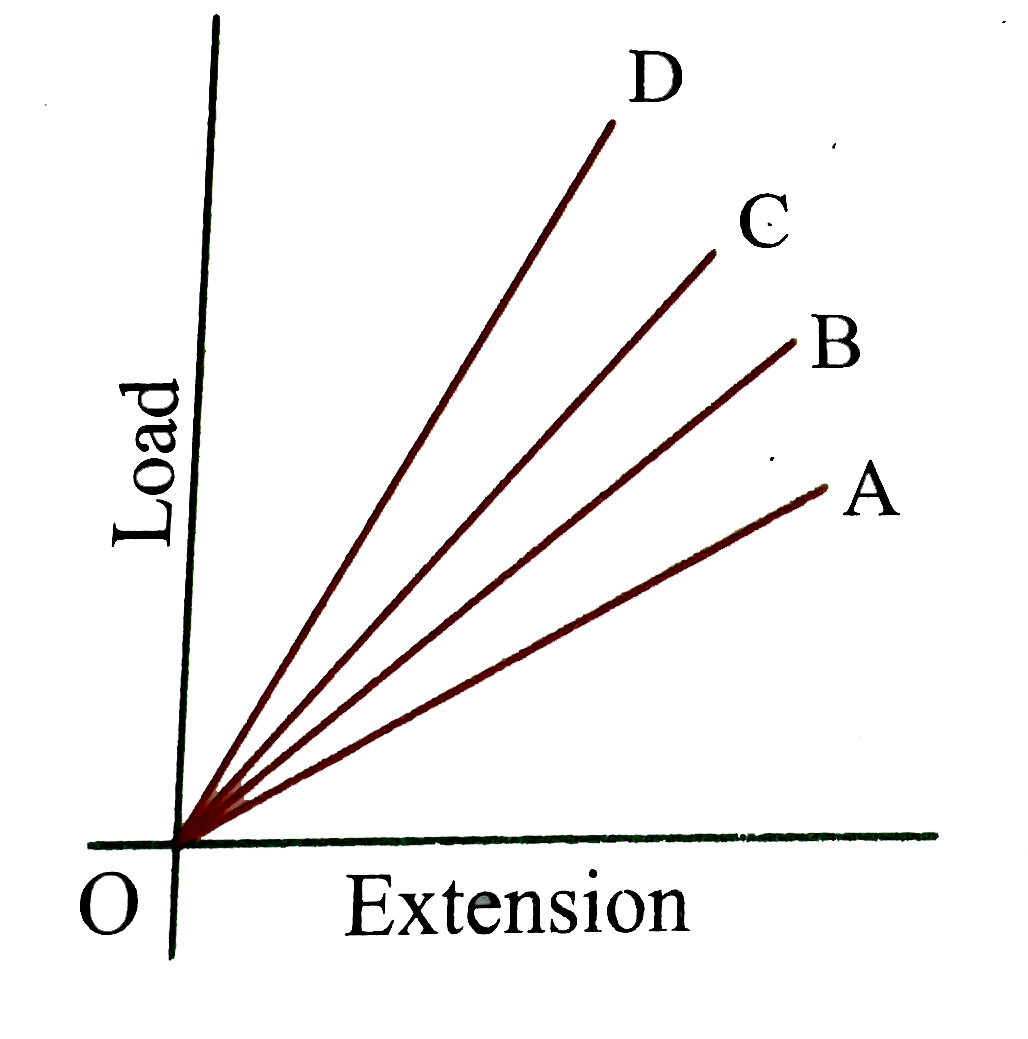 View Solution
View SolutionThe length of a wire is increased by 1mm on the application, of a given load. In a wire of the same material, but of length and radius twice that of the first, on application of the same load, extension is
View SolutionA metallic ball and highly stretched spring are made of the same material and have the same mass. They are heated so that they melt. The latent heat required
View SolutionTwo wires A and B are made of same material. The wire A has a length l and diameter r while the wire B has a length 2l and diameter r/2. If the two wires are stretched by the same force the elongation in A divided by the elongation in B is
View SolutionTwo wires A and B of same length are made of same material . The figure represents the load F versus extension Δx graph for the wires. Then
 View Solution
View SolutionA sitar wire is replaced by another wire of same length and material but of three times the earlier radius. If the tension in the wire remains the same, by what factor will the frequency change ?
View Solution

