The radii of circular orbits of two satellite A and B of the earth are 4R and R, respectively. If the speed of satellite A is 3v, then the speed of satellite B will be
3v/4
6v
12v
3v/2
The correct Answer is:B
To find the speed of satellite B, we will use the relationship between the orbital speed of a satellite and the radius of its orbit. The orbital speed v of a satellite in a circular orbit is given by the formula:
v=√GMr
where:
- G is the gravitational constant,
- M is the mass of the Earth (or the planet),
- r is the radius of the orbit.
Step 1: Identify the given values
- For satellite A:
- Radius RA=4R
- Speed vA=3v
- For satellite B:
- Radius RB=R
- Speed vB=?
Step 2: Write the expression for the orbital speeds
Using the formula for orbital speed, we can write:
vA=√GMRAandvB=√GMRB
Step 3: Substitute the known values
Substituting the values of RA and RB:
vA=√GM4RandvB=√GMR
Step 4: Relate the speeds of the satellites
From the expression for vA:
vA=√GM4R=12√GMR=12vB
Step 5: Substitute the value of vA
Since we know vA=3v:
3v=12vB
Step 6: Solve for vB
To find vB, we rearrange the equation:
vB=6v
Final Answer
The speed of satellite B is 6v.
---
- G is the gravitational constant,
- M is the mass of the Earth (or the planet),
- r is the radius of the orbit.
- For satellite A:
- Radius RA=4R
- Speed vA=3v
- Radius RB=R
- Speed vB=?
Using the formula for orbital speed, we can write:
Substituting the values of RA and RB:
From the expression for vA:
Since we know vA=3v:
To find vB, we rearrange the equation:
The speed of satellite B is 6v.
Similar Questions
Two satellites A and B go around a planet in circular orbits of radii 4 R and R respectively. If the speed of the satellite A is 3 V, then the speed of the satellite B will be
View SolutionTwo satellites P and Q go round a planet in circular orbits of radii 9R and R respectively. If the speed of the satellite P is 4V, then speed of satellite Q will be
View Solution
Knowledge Check
Two satellites orbit the Earth in circular orbits, each travelling at a constant speed. The radius of satellite A's orbit is R, and the radius of satellite B's orbit is 3R. Both satellites have the same mass. How does FA, the centripetal force on satellite A, compare with FB, the centripetal force on satellite B?
AFA=9FBBFA=3FBCFA=FBDFB=3FA
The circular orbit of two satellites have radii r1 and r2 respectively (r1<r2). If angular velosities of satellites are same, then their centripetal accelerations are related as
View SolutionThe orbital speed of geostationary satellite is around
View SolutionA satellite moves around the earth in a circular orbit with speed v. If m is the mass of the satellite, its total energy is
View SolutionTwo artificial satellites A and B are at a distance rA and rB above the earth's surface. If the radius of earth is R, then the ratio of their speed will be :-
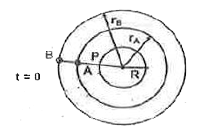
View SolutionTwo satellite A and B are travelling in the same plane and same sense in circular orbit around the earth at an atitude rA and rB from the centre of the earth respectively. If at time t=0 the satellite are aligned as shown in the figure, knowing that the radius of the earth R. Determine the time at which again the satellite will be aligned as they were at t=0
View SolutionA satelite is revolving in a circular orbit at a height h above the surface of the earth of radius R. The speed of the satellite in its orbit is one-fourth the escape velocity from the surface of the earth. The relation between h and R is
View SolutionTwo satellites A and B of the same mass are revolving around the earth in the concentric circular orbits such that the distance of satellite B from the centre of the earth is thrice as compared to the distance of the satellite A from the centre of the earth. The ratio of the centripetal force acting on B as compared to that on A is
View Solution