The circular orbit of two satellites have radii and respectively . If angular velosities of satellites are same, then their centripetal accelerations are related as
Data insufficient
The correct Answer is:C
To solve the problem, we need to relate the centripetal accelerations of two satellites in circular orbits with different radii but the same angular velocity. Let's denote the centripetal accelerations of the satellites as a1 and a2, and their respective radii as r1 and r2.
1. Understand the Formula for Centripetal Acceleration:
The centripetal acceleration a of an object moving in a circular path is given by the formula:
a=rω2
where r is the radius of the circular path and ω is the angular velocity.
2. Write the Expressions for Both Satellites:
For the first satellite with radius r1:
a1=r1ω2
For the second satellite with radius r2:
a2=r2ω2
3. Compare the Centripetal Accelerations:
Since both satellites have the same angular velocity ω, we can relate their centripetal accelerations directly through their radii:
a1a2=r1ω2r2ω2=r1r2
4. Substituting the Given Condition:
We know from the problem statement that r1<r2. Therefore, it follows that:
a1a2<1ora1<a2
5. Conclusion:
The centripetal accelerations of the two satellites are related such that:
a1<a2
Final Answer:
Thus, the centripetal accelerations of the satellites are related as a1<a2.
---
The centripetal acceleration a of an object moving in a circular path is given by the formula:
a=rω2
where r is the radius of the circular path and ω is the angular velocity.
For the first satellite with radius r1:
a1=r1ω2
For the second satellite with radius r2:
a2=r2ω2
Since both satellites have the same angular velocity ω, we can relate their centripetal accelerations directly through their radii:
a1a2=r1ω2r2ω2=r1r2
We know from the problem statement that r1<r2. Therefore, it follows that:
a1a2<1ora1<a2
The centripetal accelerations of the two satellites are related such that:
a1<a2
Thus, the centripetal accelerations of the satellites are related as a1<a2.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Taking it together67videos
CIRCULAR MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Match the columns3videos
CIRCULAR MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Integer7videos
CIRCULAR MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective21videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct27videos
COMMUNICATION SYSTEM
Similar Questions
The radii of circular orbits of two satellite A and B of the earth are 4R and R, respectively. If the speed of satellite A is 3v, then the speed of satellite B will be
View SolutionTwo cars of mass m1andm2 are moving in circle of radii r1andr2 , respectively . Their speeds are such that they make complete circles in the same time t . The ratio of their centripetal acceleration is :
View Solution
Knowledge Check
- Question 1 - Select One
Two soap bubbles A and B have radii r1andr2 respectively. If r1<r2 than the excess pressure inside
Abubbles A and B will be equalBbubbles A will be less than that in bubbles BCbubbles A will be greater than that in bubble BDbubbles A and B will be zero. - Question 2 - Select One
Two particles of equal masses are revolving in circular paths of radii, r1andr2 respectively with the same period . The ratio of their centripetal force is -
Ar1/r2B√r2/r1C(r1/r2)2D(r2/r1)2 - Question 3 - Select One
The radii of two planets are respectively R1andR2 and their densities are respectively ρ1andρ2.The ratio of the accelerations due to gravity at their surface is
AR1ρ2R2ρ1BR1ρ1R2ρ2Cρ1R22ρ2R21DR1R2ρ1ρ2
Two cars of mass m1andm2 are moving in circle of radii r1andr2 , respectively . Their speeds are such that they make complete circles in the same time t . The ratio of their centripetal acceleration is :
View SolutionThe capacitance of two concentric spherical shells of radii R1 and R2(R2>R1) is
View SolutionTwo particles of equal masses are revolving in circular paths of radii r1 and r2 respectively with the same speed. The ratio of their centripetal force is
View SolutionTwo satellite A and B are travelling in the same plane and same sense in circular orbit around the earth at an atitude rA and rB from the centre of the earth respectively. If at time t=0 the satellite are aligned as shown in the figure, knowing that the radius of the earth R. Determine the time at which again the satellite will be aligned as they were at t=0
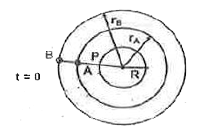 View Solution
View SolutionTwo resistors A and B have resistances RAandRBrespectively with RA<RB.the resistivities of their materials are (ρA)and(ρB).
View Solution

