A roller coaster is designed such that riders experience "weightlessness" as they go round the top of a hill whose radius of curvature is 20m. The speed of the car at the top of the hill is between
14m/s and 15m/s
15m/s and 16m/s
16m/s and 17m/s
13m/s and 14m/s
The correct Answer is:A
To solve the problem of determining the speed of a roller coaster at the top of a hill where riders experience weightlessness, we can follow these steps:
Step 1: Understand the Forces Acting on the Rider
At the top of the hill, two main forces act on the rider:
- The gravitational force (weight) acting downward, which is mg.
- The normal force acting upward, which is N.
Step 2: Set Up the Equation for Weightlessness
For the rider to experience weightlessness, the normal force N must be zero. Therefore, the gravitational force must provide the necessary centripetal force to keep the rider moving in a circular path. This gives us the equation:
mg−N=mv2r
Since N=0 for weightlessness, we can simplify the equation to:
mg=mv2r
Step 3: Cancel the Mass m
Since the mass m appears on both sides of the equation, we can cancel it out:
g=v2r
Step 4: Rearrange to Solve for Speed v
Rearranging the equation gives us:
v2=gr
Taking the square root of both sides, we find:
v=√gr
Step 5: Substitute the Given Values
We are given:
- The radius of curvature r=20m
- The acceleration due to gravity g≈9.8m/s2 (or we can use g≈10m/s2 for simplicity)
Using g=10m/s2:
v=√10×20=√200
Step 6: Calculate the Speed
Calculating √200:
√200=√100×2=10√2≈14.14m/s
Step 7: Determine the Range of Speed
Since the question asks for the speed range, we can conclude that the speed of the roller coaster at the top of the hill is approximately between 14 m/s and 15 m/s.
Final Answer
The speed of the car at the top of the hill is between 14 m/s and 15 m/s.
---
At the top of the hill, two main forces act on the rider:
- The gravitational force (weight) acting downward, which is mg.
- The normal force acting upward, which is N.
For the rider to experience weightlessness, the normal force N must be zero. Therefore, the gravitational force must provide the necessary centripetal force to keep the rider moving in a circular path. This gives us the equation:
mg−N=mv2r
Since N=0 for weightlessness, we can simplify the equation to:
mg=mv2r
Since the mass m appears on both sides of the equation, we can cancel it out:
g=v2r
Rearranging the equation gives us:
v2=gr
Taking the square root of both sides, we find:
v=√gr
We are given:
- The radius of curvature r=20m
- The acceleration due to gravity g≈9.8m/s2 (or we can use g≈10m/s2 for simplicity)
v=√10×20=√200
Calculating √200:
√200=√100×2=10√2≈14.14m/s
Since the question asks for the speed range, we can conclude that the speed of the roller coaster at the top of the hill is approximately between 14 m/s and 15 m/s.
The speed of the car at the top of the hill is between 14 m/s and 15 m/s.
Similar Questions
A roller-coaster car enters the circular-loop part of the ride. At the very top of the circle (where the people in the car are upside down), the speed of the car is v and the acceleration points straight down. If the radius of the loop is r and the total mass of the car (plus passenger) is m, find the magnitude of the normal force exerted by the track on the car at this point.
View SolutionA car moves at a constant speed on a straigh but hilly road. One section has a crest and dip of the 250m radius.
(a) As the car passes over the crest the normal force on the car is half the 16kN weight of the car. What will the noraml force on the car its passes through th ebottom of the dip?
(b) What is the greatest speed at which the car can move without leaving the road at the top of the hill ?
(c) Moving at a speed found in part (b) what will be the normal force on the car as it moves through the bottom of the dip? (Take, g=10m/s2)
View SolutionTwo guns situated at the top of a hill of height 10m fire one shot each with the same speed 5√3m/s at some interval of time. One gun fires horizontal and the other fores upwards at an angle of 60∘ with the horizontal. Two shots collide in air at a point P. Find (i) time-interval between the firing and (ii) coordinates of the point P. Take the origin of coordinates system at the foot of the hill right below the muzzle and trajectorise in the x−y plane.
View SolutionA small toy car moves round a circular track of radius 4 m. The car makes one revolution in 10 s. Calculate (a) the speed of the car, (b) its centripetal acceleration, (c) the centripetal force exerted,by the track if the.mass of the car is 200 g, (d) the safe speed with which the car can move around without toppling, if the distance between the wheels is 4 cm and the height of the centre of gravity of the car from the horizontal is 2 cm.
View SolutionTwo guns situated at the top of a hill of height 10m fire one shot each with the same speed 5√3m/s at some interval of time. One gun fires horizontal and the other fores upwards at an angle of 60∘ with the horizontal. Two shots collide in air at a poit P. Find (i) time-interval between the firing and (ii) coordinates of the point P. Take the origin of coordinates system at the foot of the hill right below the muzzle and trajectorise in the x−y plane.
View SolutionA train is moving with a speed of 20 m/s at a place where the radius of curvature of the railway line is 1500 m. Calculate the distance between the rails if the elevation of the outer rail above the inner rail is 0.042 m ?
View SolutionA car travelling towards a hill at 10m/s sound its horn which a frequency 500HZ. This is heard in a second car travelling behind the first car in the same direction with speed 20m/s. The sound can also be heard in the second car by reflections of sound the hill. The beat frequency heard by the driver of the sound car will be (speed of sound in air =340m/s)
View SolutionA block of mass m at the end of a string is whirled round in a vertical circle of radius R. The critical speed of the block at top of its swing below which the string would slacken before the block reaches the bottom is?
View SolutionName the type of waves which are used for line of sight (LOS) communication. What is the range of their frequencies?
A transmitting antenna at the top of a tower has a height of 20m and the height of the receiving antenna is 45m. Calculate the maximum distance between them for satisfactory communication in LOS mode. (Radius of the Earth =6.4×106 m)
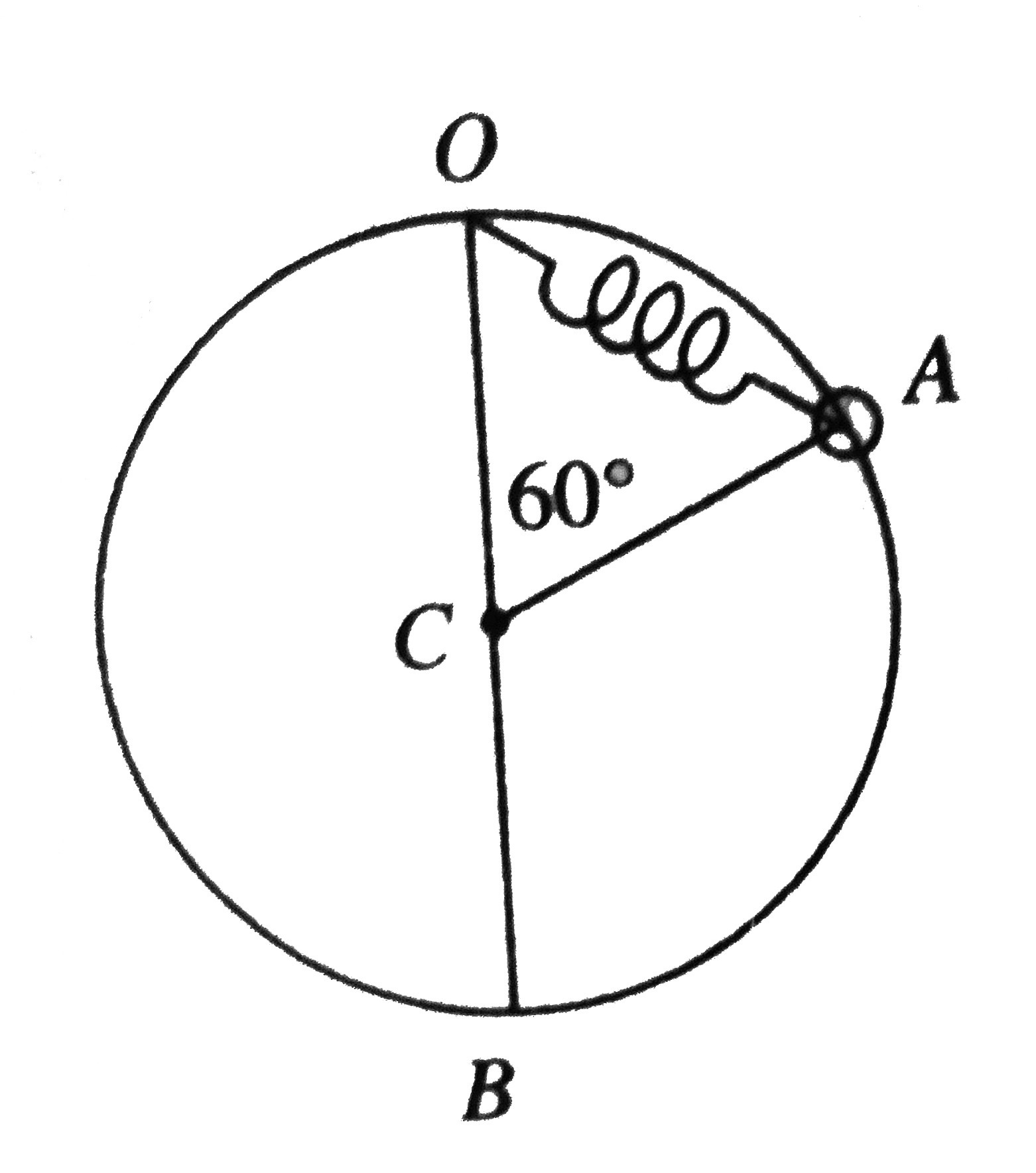
View SolutionA particle of mass 5kg is free to slide on a smooth ring of radius r=20cm fixed in a vertical plane. The particle is attached to one end of a spring whose other end is fixed to the top point O of the ring. Initially, the particle is at rest at a point A of the ring such that ∠OCA=60∘, C being the centre of the ring. The natural length of the spring is also equal to r=20cm. After the particle is released and slides down the ring, the contact force between the particle and the ring becomes zero when it reaches the lowest position B. Determine the force constant (in×102Nm−1) of the spring.
View Solution
