A rubber ball is dropped from a height of 5mon a plane, where the acceleration due to gravity is not shown. On bouncing it rises to 1.8m. The ball loses its velocity on bouncing by a factor of
16/25
2/5
3/5
9/25
The correct Answer is:B
To solve the problem of how much velocity the rubber ball loses on bouncing, we can follow these steps:
Step 1: Determine the initial velocity before impact
When the ball is dropped from a height h1=5m, we can calculate the velocity just before it hits the ground using the formula for gravitational potential energy converted to kinetic energy:
v1=√2gh1
Step 2: Calculate the height after bouncing
After bouncing, the ball rises to a height h2=1.8m. The velocity just after the bounce can be calculated using the same formula:
v2=√2gh2
Step 3: Find the ratio of the velocities
To find the factor by which the ball loses its velocity, we need to calculate the ratio of the velocities v2 and v1:
v2v1=√2gh2√2gh1=√h2h1
Step 4: Substitute the heights into the ratio
Substituting the values of h1 and h2:
v2v1=√1.85=√1850=√925=35
Step 5: Calculate the loss in velocity
The loss in velocity can be expressed as:
Loss factor=1−v2v1=1−35=25
Conclusion
The ball loses its velocity on bouncing by a factor of 25.
---
When the ball is dropped from a height h1=5m, we can calculate the velocity just before it hits the ground using the formula for gravitational potential energy converted to kinetic energy:
After bouncing, the ball rises to a height h2=1.8m. The velocity just after the bounce can be calculated using the same formula:
To find the factor by which the ball loses its velocity, we need to calculate the ratio of the velocities v2 and v1:
Substituting the values of h1 and h2:
The loss in velocity can be expressed as:
The ball loses its velocity on bouncing by a factor of 25.
Similar Questions
Knowledge Check
An inelastic ball is dropped from a height of 100 m. Due to earth 20% of its energy is lost. To what height the ball will rise ?
A80 mB40 mC60 mD20 m
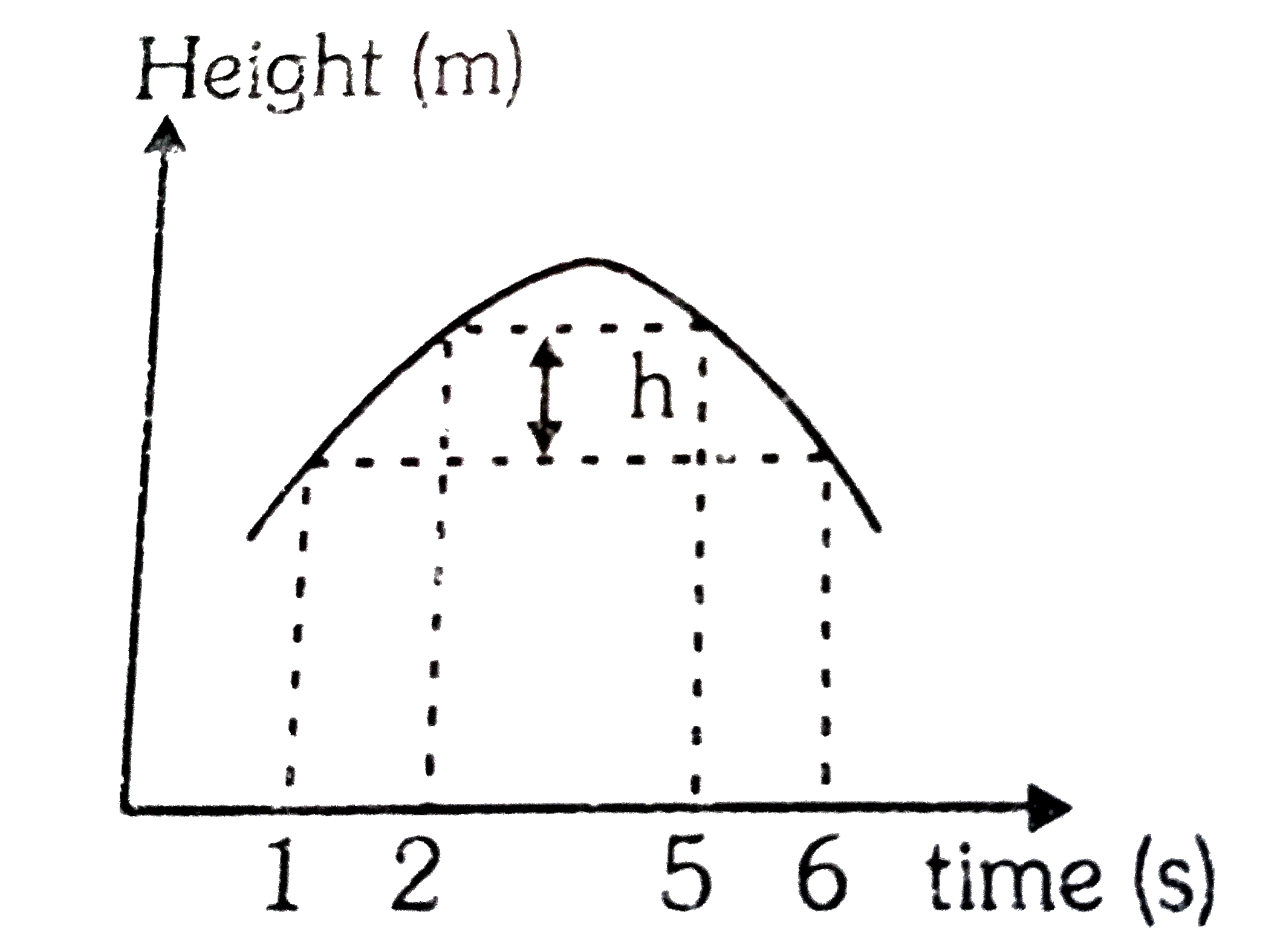
A ball is thrown upwards . Its height varies with time as shown in figure. If the acceleration due to gravity is 7.5m/s2, then the height h is
View SolutionA ball dropped from a height of 2 m rebounds to a height of 1.5 m after hitting the ground. Then fraction of energy lost is
View SolutionTwo balls are dropped from the same height at two different places A and B where the acceleration due to gravities are gAandgB. The body at 'B' takes 't' seconds less to reach the ground and strikes the ground with a velocity greater than at 'A' by υm/s. Then the value of υ/t is
View SolutionA ball is dropped onto a floor from a height of 10m. If 20% of its initial energy is lost,then the height of bounce is
View SolutionA ball is dropped from a height of 5 m, if it rebound upto height of 1.8 m, then the ratio of velocities of the ball after and before rebound is :
View SolutionA ball of mass 1kg is dropped from a height of 3.2m on smooth inclined plane. The coefficient of restitution for the collision is e=1/2. The ball's velocity become horizontal after the collision.

View SolutionA ball is dropped from a height of 49 m. The wind is blowing horizontally. Due to wind a constant horizontal acceleration is provided to the ball. Choose the correct statement (s).
View Solution
