The amplitude of a simple pendulum is 10 cm. When the pendulum is at a displacement of 4 cm from the mean position, the ratio of kinetic and potential energies at that point is
5.25
2.5
4.5
7.5
The correct Answer is:A
To find the ratio of kinetic energy (KE) to potential energy (PE) of a simple pendulum at a given displacement, we can follow these steps:
Step 1: Understand the formulas for Kinetic and Potential Energy
In simple harmonic motion (SHM), the kinetic energy (KE) and potential energy (PE) of a pendulum are given by the following formulas:
- Kinetic Energy (KE) = 12mω2(A2−y2)
- Potential Energy (PE) = 12mω2y2
Where:
- m = mass of the pendulum bob (which will cancel out)
- ω = angular frequency
- A = amplitude of the pendulum
- y = displacement from the mean position
Step 2: Substitute the known values
Given:
- Amplitude A=10 cm
- Displacement y=4 cm
Step 3: Calculate the ratio of KE to PE
To find the ratio KEPE, we can substitute the formulas into the ratio:
KEPE=12mω2(A2−y2)12mω2y2
Step 4: Simplify the expression
The 12mω2 terms will cancel out:
KEPE=A2−y2y2
Step 5: Substitute the values of A and y
Now substitute A=10 cm and y=4 cm:
KEPE=102−4242=100−1616=8416
Step 6: Simplify the ratio
Now simplify 8416:
8416=214=5.25
Conclusion
Thus, the ratio of kinetic energy to potential energy at a displacement of 4 cm from the mean position is 5.25.
In simple harmonic motion (SHM), the kinetic energy (KE) and potential energy (PE) of a pendulum are given by the following formulas:
- Kinetic Energy (KE) = 12mω2(A2−y2)
- Potential Energy (PE) = 12mω2y2
- m = mass of the pendulum bob (which will cancel out)
- ω = angular frequency
- A = amplitude of the pendulum
- y = displacement from the mean position
Given:
- Amplitude A=10 cm
- Displacement y=4 cm
To find the ratio KEPE, we can substitute the formulas into the ratio:
The 12mω2 terms will cancel out:
Now substitute A=10 cm and y=4 cm:
Now simplify 8416:
Thus, the ratio of kinetic energy to potential energy at a displacement of 4 cm from the mean position is 5.25.
Similar Questions
The amgular velocity and the amplitude of a simple pendulum is ω and a respectively. At a displacement x from the mean position, if its kinetic energy is T and potential energy is U, then the ratio of T to U is
View SolutionThe figure below shows a simple pendulum of mass 200 g. It is displaced from the mean position A to the extreme position B. The potential energy at the position A is zero. At the position B the pendulum bob is raised by 5 m.
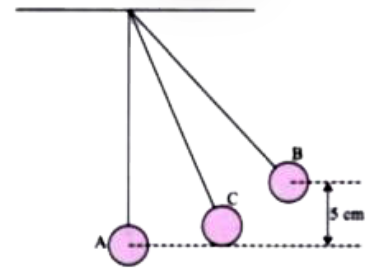
(i) What is the potential energy of the pendulum at the position B?
(ii) What is the total mechanical energy at point C?
(iii) What is the speed of the bob at the position A when released from B ?
(Take g = 10ms−2 and there is no loss of energy.)
View SolutionThe length of the simple pendulum is 40 cm. Calculate its time period.
View SolutionA particle executes simple harmonic motion with an amplitude of 10 cm. At what distance from the mean position are the kinetic and potential energies equal?
View SolutionThe total energy of a simple pendulum is x. When the displacement is half of amplitude,its KE will be
View SolutionIf A is amplitude of a particle in SHM, its displacement from the mean position when its kinetic energy is thrice that to its potential energy
View SolutionA certain simple harmonic vibrator of mass 0.1 kg has a total energy of 10 J. Its displacement from the mean position is 1 cm when it has equal kinetic and potential energies. The amplitude A and frequency n of vibration of the vibrator are
View SolutionA particle executes SHM with amplitude A and time period T. When the displacement from the equilibrium position is half the amplitude , what fractions of the total energy are kinetic and potential energy?
View SolutionA particle excutes simple harmonic motion with an amplitude of 5 cm. When the particle is at 4 cm from the mean position, the magnitude of its velocity in SI units is equal to that of its acceleration. Then, its periodic time in seconds is
View SolutionA particle executes linear simple harmonic motion with an amplitude of 3cm. When the particle is at 2cm from the mean position, the magnitude of its velocity is equal to that of its acceleration. Then, its time period in seconds is
View Solution
