9.8m/s
The correct Answer is:d
To solve the problem step by step, we need to clarify the context of the question. It seems like we are multiplying several velocities given in meters per second (m/s). Here’s how we can approach this:
1. Identify the quantities: We have four velocities given:
- v1=9.8m/s
- v2=10m/s
- v3=5.8m/s
- v4=17.3m/s
2. Multiply the velocities: Since we are multiplying these velocities together, we can express this as:
vtotal=v1×v2×v3×v4
3. Perform the multiplication:
vtotal=9.8×10×5.8×17.3
4. Calculate step by step:
- First, multiply 9.8×10=98
- Next, multiply 98×5.8=568.4
- Finally, multiply 568.4×17.3=9833.32
5. Combine the units: Since we are multiplying velocities (m/s), the resulting unit will be:
m/s×m/s×m/s×m/s=m4/s4
6. Final Result: The final result of the multiplication is:
vtotal=9833.32m4/s4
- v1=9.8m/s
- v2=10m/s
- v3=5.8m/s
- v4=17.3m/s
vtotal=v1×v2×v3×v4
vtotal=9.8×10×5.8×17.3
- First, multiply 9.8×10=98
- Next, multiply 98×5.8=568.4
- Finally, multiply 568.4×17.3=9833.32
m/s×m/s×m/s×m/s=m4/s4
vtotal=9833.32m4/s4
Similar Questions
Knowledge Check
A body is thrown with a velocity of 9.8 m/s making an angle of 30∘ with the horizontal. It will hit the ground after a time
A3 sB2sC1.5 sD1 s
The length of a simple pendulum is 39.2/π2 m. If g=9.8m/s2 , the value of time period is
View SolutionA Sphere pure rolls on a rough inclined plane with initial velocity 2.8 m/s. Find the maximum distance on the inclined plane

View SolutionIf g on the surface of the earth is 9.8m/s2, find its value at a height of 6400 km.
(Radius of the earth = 6400 km)
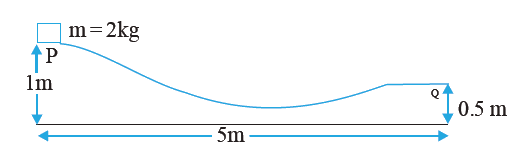
View SolutionFind the horizontal velocity of the particle when it reach the point Q. Assume the block to be frictionless. Take g=9.8m/s2.
View SolutionA 10 kg steel ball is suspended by two strings as shown. The tensions in the two strings are: (g=9.8 m/s2)

View SolutionA body is projected with an initial velocity of 58.8 m/s at angle 60° with the vertical. The vertical component of velocity after 2 sec is
View SolutionA body is projected horizontally from the top of a hill with a velocity of 9.8 m/s. What time elapses before the vertical velocity is twice the horizontal velocity?
View Solution
