A Sphere pure rolls on a rough inclined plane with initial velocity 2.8 m/s. Find the maximum distance on the inclined plane

2.74 m
5.48 m
1.38 m
3.2 m
The correct Answer is:A
a=gsinθ1+k2/r2
I=25mr2=mk2
k2r2=25
a=gsinθ1+2/5
2.82=2g×1272×S
S=2.82×720
S=2.744m
Similar Questions
A particle is projected from the inclined plane at angle 37∘ with the inclined plane in upward direction with speed 10m/s. The angle of inclined plane with horizontal is 53∘. Then the maximum height attained by the particle from the inclined plane will be-
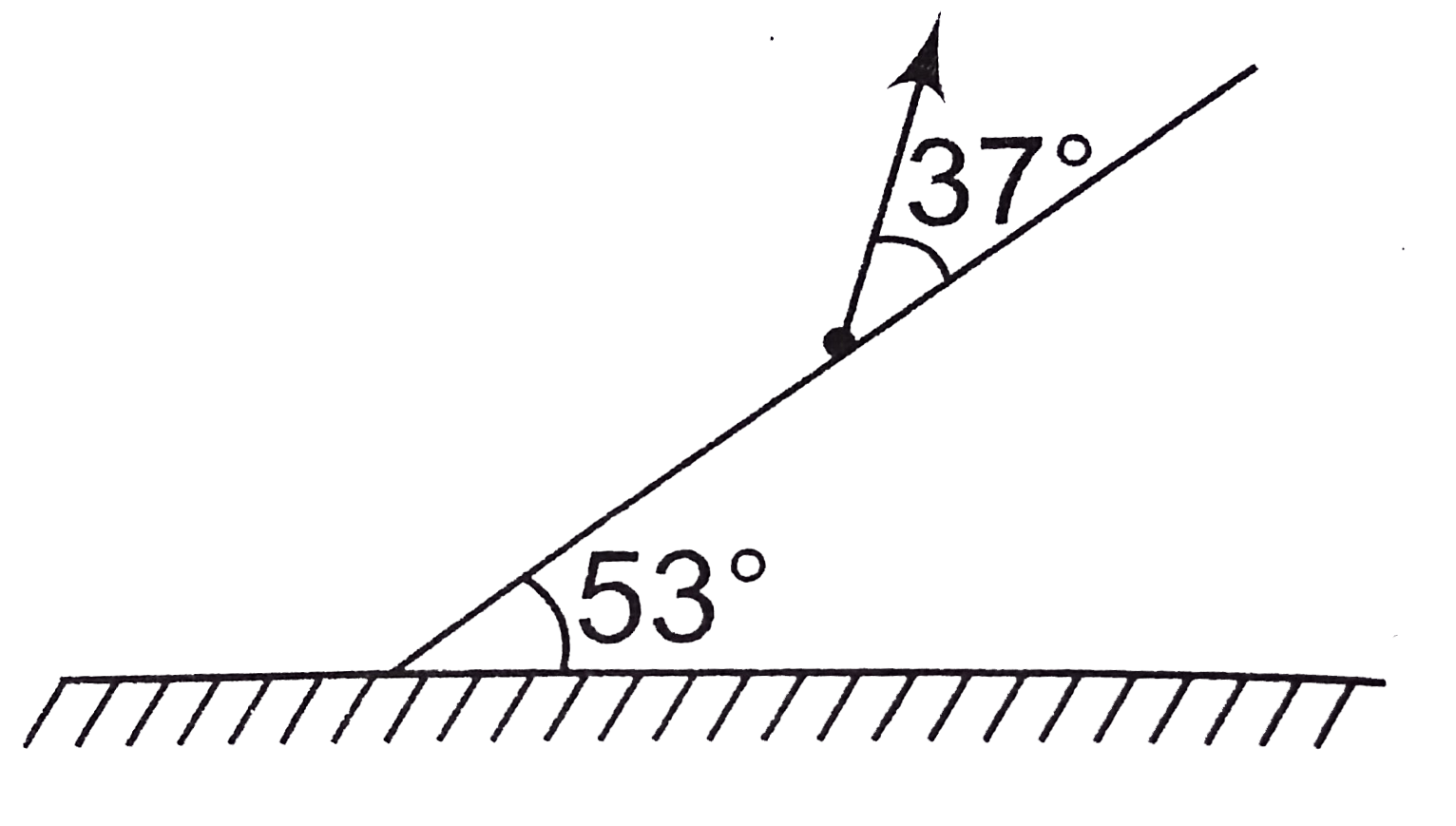
View SolutionA block kept on a rough inclined plane, as shown in the figure, remains at rest upto a maximum force 2N down the inclined plane. The maximum external force up the inclined plane that does not move the block is 10N. The coefficient of static friction between the block and the plane is : : [Taking g=10m/s2].

View SolutionBlock of mass 10 kg is moving on inclined plane with constant velocity 10 m/s. The coedfficient of kinetic friction between incline plane and block is :-
View SolutionA solid cylinder is rolling down a rough inclined plane of inclination θ. Then
View SolutionA ring rolls down an inclined plane and acquires a velocity v upon reaching the bottom of the inclined plane. If another body rolls down from the same height over the same inclined plane and acquires a velocity √65v upon reaching the bottom of the inclined plane, then that body is
View SolutionA particle of mass 5kg is moving on rough fixed inclined plane with constant velocity of 5m/s as shown in the figure. Find the friction force acting on a body by plane.

View SolutionA solid cylinder and a solid sphere, both having the same mass and radius, are released from a rough inclined plane of inclination θ one by one. They roll on the inclined plane without slipping. The force of friction that acts
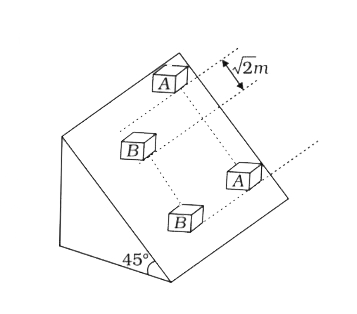
View SolutionTwo identical blocks A and B of equal masses are placed on rough inclined plane as shown in the figure. Initially the block A is √2m behind the block B. Coefficient of kinetic friction for the blocks A and B are 0.2 and 0.3 respectively (g=10m/s2). By the time the two blocks come on the same line on the inclined plane if they are released simultaneously, the distance moved by B is βm Find the value of β
View SolutionIn figure, the angle of inclination of the inclined plane is 30∘. Find the horizontal velocity V0 so that the particle hits the inclined plane perpendicularly.
 .
.
View SolutionA hollow sphere rolls down a rough inclined plane whose angle of inclination is θ, with horizontal. For the hollow sphere to undergo pure rolling, without slipping, the condition is [μ = coefficient of friction between the hollow sphere and inclined plane]
View Solution
