An electric fan has blades of length 30 cm neasured from the axis of rotation. If the fan rotating at 120 rev/min. the acceleration of a point on the tip of the blade is
(a) 1600ms−2
(b) 47.4ms−2
(c) 23.7ms−2
(d) 50.55ms−2
1600ms−2
47.4ms−2
23.7ms−2
50.55ms−2
The correct Answer is:b
To solve the problem of finding the acceleration of a point on the tip of the blade of an electric fan, we can follow these steps:
1. Identify the Given Data:
- Length of the blade (radius, r) = 30 cm = 0.3 m
- Rotational speed = 120 revolutions per minute (rev/min)
2. Convert Revolutions per Minute to Revolutions per Second:
Frequency(f)=120 rev/min60 s/min=2 rev/s
3. Calculate Angular Velocity (ω):
The angular velocity in radians per second can be calculated using the formula:
ω=2πf
Substituting the value of f:
ω=2π×2=4π rad/s
4. Calculate Centripetal Acceleration (ac):
The formula for centripetal acceleration is given by:
ac=ω2r
Substituting the values of ω and r:
ac=(4π)2×0.3
5. Calculate (4π)2:
(4π)2=16π2
Using π≈227:
π2≈(227)2=48449
Thus,
16π2≈16×48449=774449
6. Calculate the Centripetal Acceleration:
Now substituting back into the centripetal acceleration formula:
ac=774449×0.3=2323.249≈47.4 m/s2
7. Final Result:
The acceleration of a point on the tip of the blade is approximately 47.4 m/s2.
Conclusion:
The correct answer is (b) 47.4 m/s2.
---
- Length of the blade (radius, r) = 30 cm = 0.3 m
- Rotational speed = 120 revolutions per minute (rev/min)
Frequency(f)=120 rev/min60 s/min=2 rev/s
The angular velocity in radians per second can be calculated using the formula:
ω=2πf
Substituting the value of f:
ω=2π×2=4π rad/s
The formula for centripetal acceleration is given by:
ac=ω2r
Substituting the values of ω and r:
ac=(4π)2×0.3
(4π)2=16π2
Using π≈227:
π2≈(227)2=48449
Thus,
16π2≈16×48449=774449
Now substituting back into the centripetal acceleration formula:
ac=774449×0.3=2323.249≈47.4 m/s2
The acceleration of a point on the tip of the blade is approximately 47.4 m/s2.
The correct answer is (b) 47.4 m/s2.
Similar Questions
An electric fan has blades of length 30cm as measured from the axis of rotation. If the fan is rotating at 1200 rpm, find the acceleration of a point on the tip of a blade.
View SolutionFor shown situation draw a graph showing acceleration of A and B on y-axis and time on x-axis (g=10ms−2)

View SolutionA liquid is flowing through horizonatal pipes as shown in figure. The value of speed v is
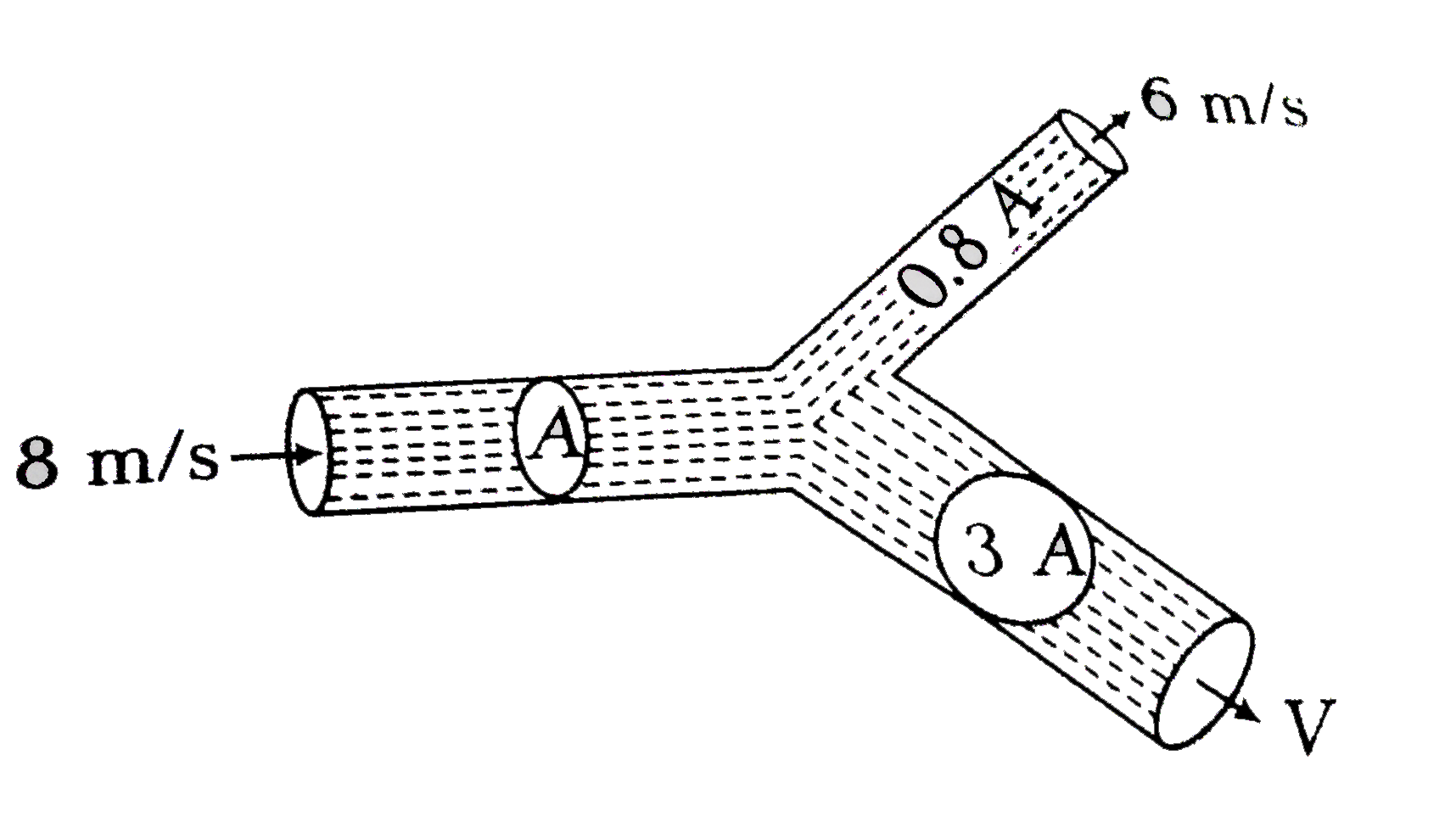
(a)1.1ms−1 (b)2.1ms−1
(c)3.1ms−1 (d)5.1ms−1
View SolutionA clock has a continuously moving second's hand of 0.1 m length. The average acceleration of the tip of the hand (in units of ms−2) is of the order of :
View SolutionThe distance travelled by a particle starting from rest and moving with an acceleration 43ms−2, in the third second is.
View SolutionThe distance travelled by a particle starting from rest and moving with an acceleration 43ms−2, in the third second is.
View SolutionA body starts at t=0 with velcoity u and travels along a straight linge. The body has a constant acceleration(a). Draw the acceleration-time graph from t=0 to t=10s for the following cases:
a. u=8ms−1, a=2s^(-2)<br>b.u=8 ms^(-1),a=−2ms−2
c. u=−8ms−1 ,a=2 ms^(-2)<br>d.u=-8ms^(-1),a=−2ms−2.
View SolutionA bullet emerges from a barrel of length 1.2m with a speed of 640ms1. Assuming constant acceleration, after the gun is fired is
View SolutionA body is projected horizontally from the top of a tower with a velocity of 30 m/s. The velocity of the body 4 seconds after projection is (g = 10ms−2)
View SolutionIn the adjacent figure, mass of A, B and C are 1 kg , 3 kg and 2 kg, respectively. Find

(a) the acceleration of the system, and
(b) tensions in the string .
Neglect friction. (g=10ms−2)
View Solution