An electric fan has blades of length 30cm as measured from the axis of rotation. If the fan is rotating at 1200 rpm, find the acceleration of a point on the tip of a blade.
The correct Answer is:480π2ms−2
To solve the problem of finding the acceleration of a point on the tip of a blade of an electric fan, we can follow these steps:
Step 1: Convert the rotational speed from RPM to radians per second
The fan is rotating at 1200 revolutions per minute (RPM). To convert this to radians per second (rad/s), we use the conversion factor that 1 revolution is equal to 2π radians and there are 60 seconds in a minute.
ω=1200rpm×2πradians1revolution×1minute60seconds
Calculating this gives:
ω=1200×2π60=40πrad/s
Step 2: Identify the radius of rotation
The length of the fan blades is given as 30 cm. To use this in our calculations, we need to convert it to meters:
R=30cm=0.3m
Step 3: Calculate the centripetal acceleration
The formula for centripetal acceleration a at the tip of the blade is given by:
a=ω2R
Substituting the values we calculated:
a=(40π)2×0.3
Step 4: Simplify the expression
Calculating (40π)2:
(40π)2=1600π2
Now substituting this back into the acceleration formula:
a=1600π2×0.3=480π2m/s2
Step 5: Approximate π2
Using π2≈10 for approximation:
a≈480×10=4800m/s2
Thus, the acceleration of a point on the tip of the blade is approximately 4800m/s2.
Final Answer:
The acceleration of a point on the tip of a blade is approximately 4800m/s2.
---
The fan is rotating at 1200 revolutions per minute (RPM). To convert this to radians per second (rad/s), we use the conversion factor that 1 revolution is equal to 2π radians and there are 60 seconds in a minute.
The length of the fan blades is given as 30 cm. To use this in our calculations, we need to convert it to meters:
The formula for centripetal acceleration a at the tip of the blade is given by:
Calculating (40π)2:
Using π2≈10 for approximation:
The acceleration of a point on the tip of a blade is approximately 4800m/s2.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Single Correct76videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Multiple Correct11videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.411videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer9videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression2videos
KINETIC THEORY OF GASES
Similar Questions
An electric fan has blades of length 30 cm neasured from the axis of rotation. If the fan rotating at 120 rev/min. the acceleration of a point on the tip of the blade is
(a) 1600ms−2 (b) 47.4ms−2 (c) 23.7ms−2 (d) 50.55ms−2View SolutionA ring of radius R is rotating about axis of ring such that angular velocity is given as = 5t. Find acceleration of a point P on rim after 5 sec
View SolutionA solenoid of length 8cm has 500 turns /m in it. If radius of coil is 3cm and if it is carrying a current of 2A, find the magnetic induction at a point 4cm from the end on the axis of the solenoid
View SolutionTen seconds after an electric fan is turned on, the fan rotates at 300 rev/min. Its average angular acceleration is
View SolutionA light ray I is incident on a plane mirror M.The mirror is rotated in the direction as shown in the figure by an arrow at frequency 9πrev/sec,The light reflected by the mirror is received on the wall W at a distance 10mfrom the axis of rotation .When the angle of incidence becomes 37∘find the speed of the spot (a point) on the wall?
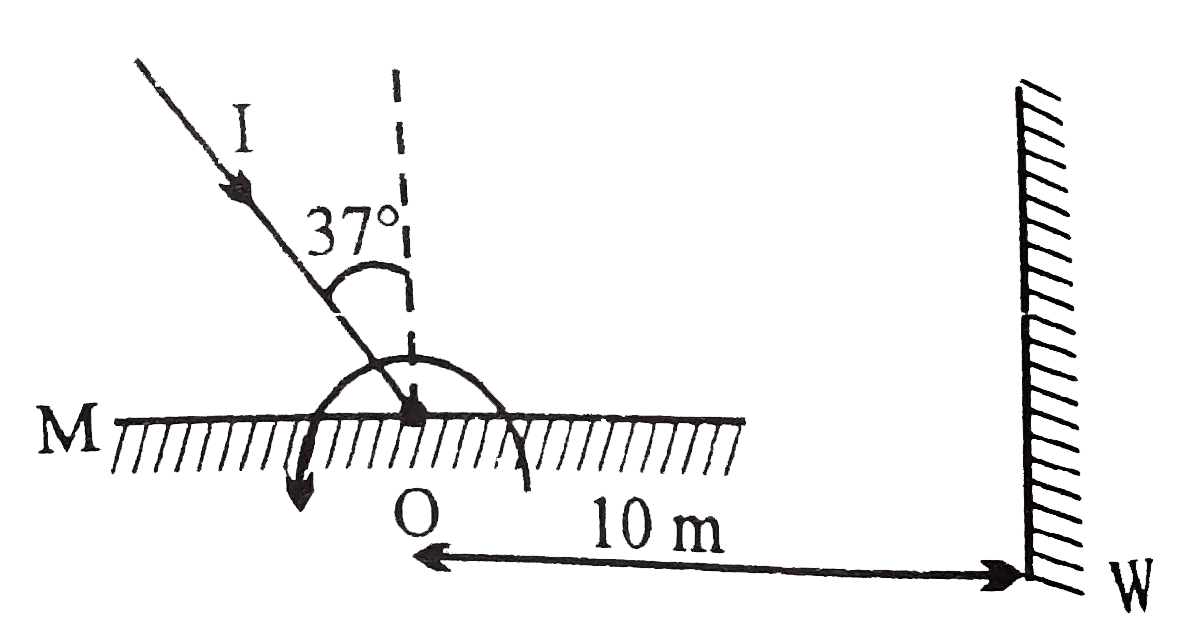 View Solution
View SolutionA solenoid of length 10 cm and radius 1 cm contains 200 turns and carries a current of 10 A. Find the magnetic field at a point on the axis at a distance of 10cm from the centre.
View SolutionWhen a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
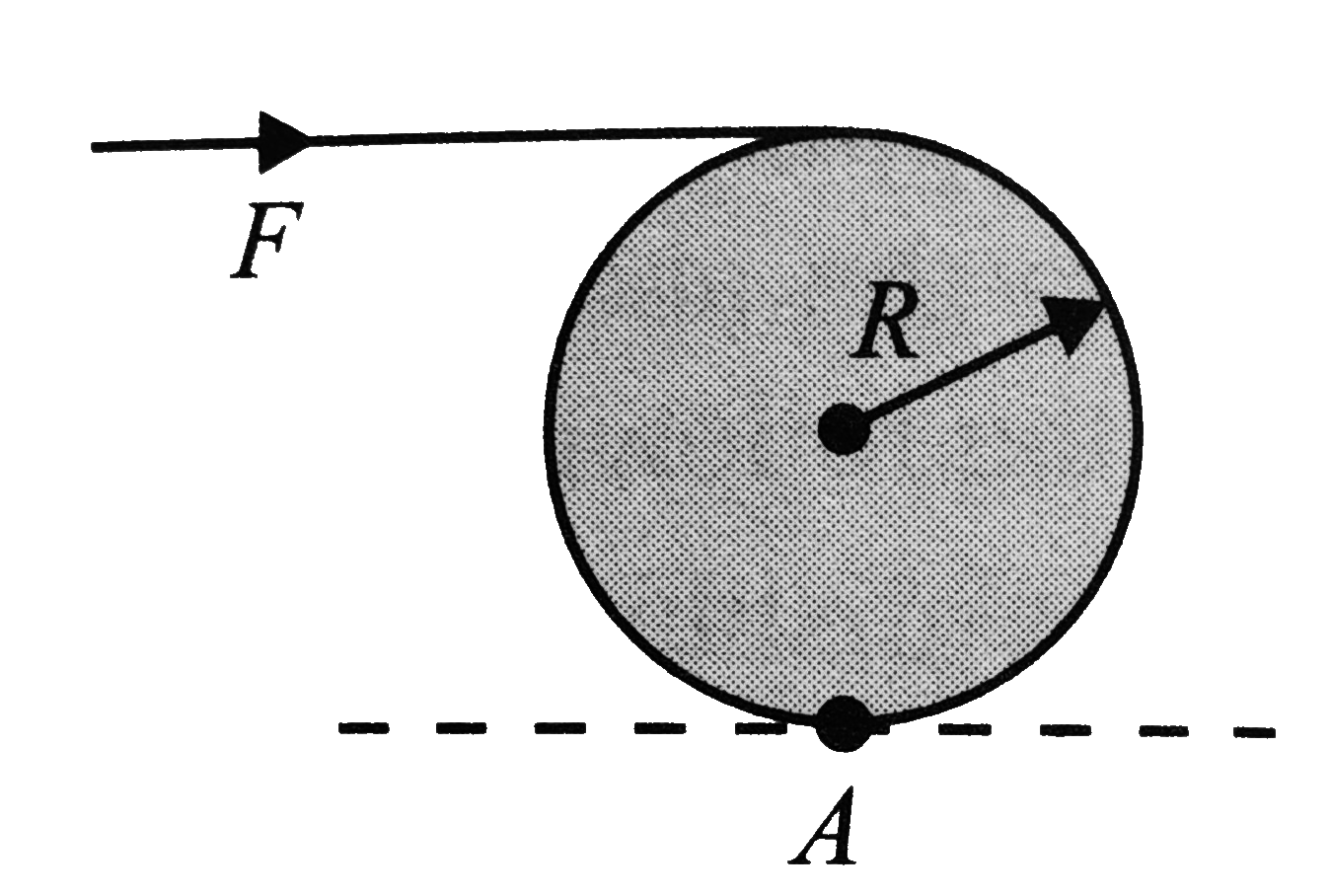
Tangential acceleration of the centre of mass isView SolutionA uniform disc rotating freely about a vertical axis makes 90 rpm. A small piece of wax of mass m gram falls vertically on the disc and sticks to it at a distance rcm from the axis. If number of rotations per minute reduces to 60, find the moment of inertia of the disc.
View SolutionThe electric intensity due to a dipole of length 10cm and having a charge of 500μC, at a point on the axis at a distance 20cm from one of the charges in air is
View SolutionFigure shows as rod of length 20 cm pivoted near an end and which is made to rotate in a horizontal plane with a constant angular speed. A ball ofmass m is spuspended by a string angular also of length 20 cm from the other end of the rod. If the angle θ made by the stirng with the vertical is 300. find the anglular speed of the rotation. Take g=10ms2
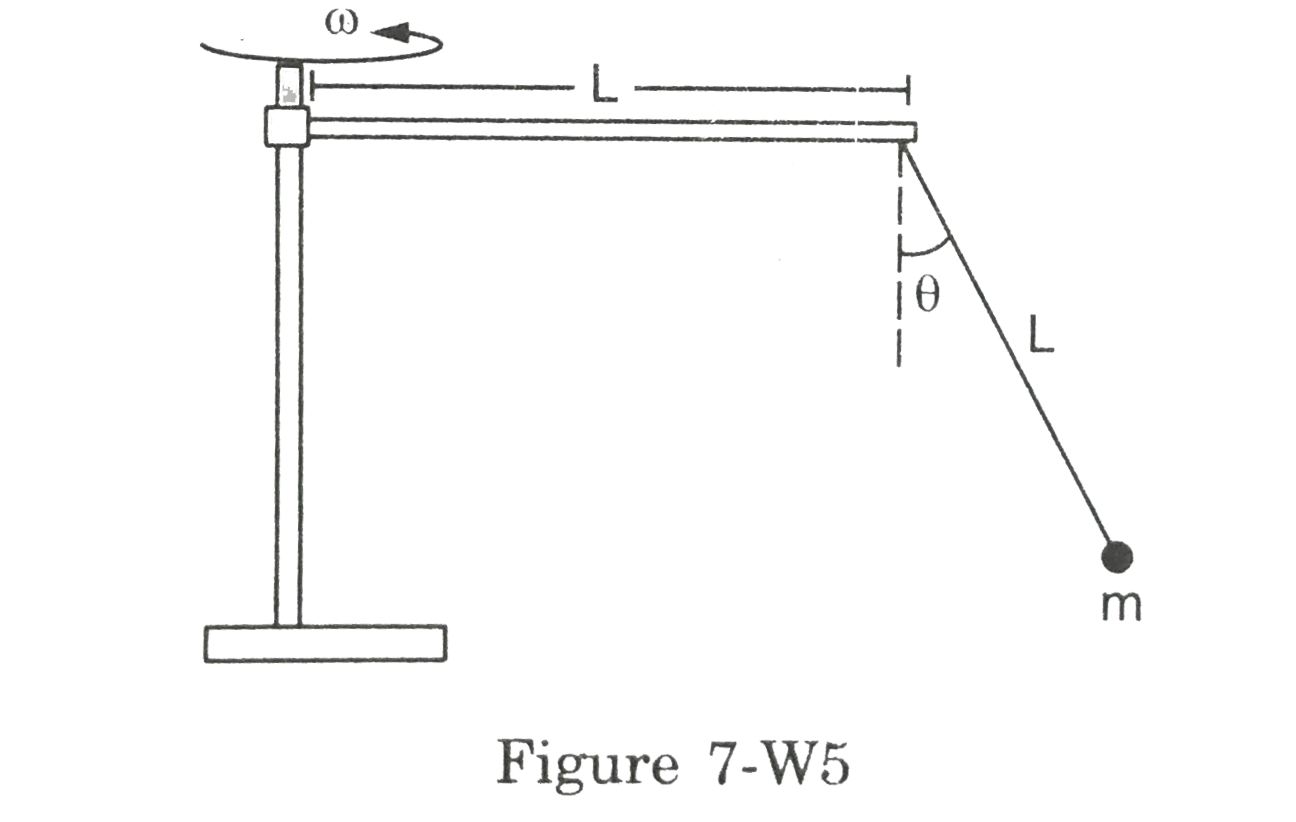 View Solution
View Solution

