A capacitor is charged by a battery. The battery is removed and another identical uncharged capacitor is connected in parallel. The total electrostatic energy of resulting system:
increases by a factor of 4
decreases by a factor of 2
remains the same
increases by a factor of 2
The correct Answer is:D
To solve the problem, we need to analyze the situation step by step.
Step 1: Understand the Initial Conditions
We have one capacitor (let's call it C1) that is charged by a battery to a voltage V. The charge on this capacitor can be calculated using the formula:
Q=C⋅V
where C is the capacitance of the capacitor.
Hint: Remember that the charge on a capacitor is directly proportional to the capacitance and the voltage across it.
Step 2: Calculate the Initial Energy
The electrostatic energy (Ui) stored in the charged capacitor can be calculated using the formula:
Ui=12CV2
Hint: The energy stored in a capacitor is given by the formula involving capacitance and the square of the voltage.
Step 3: Connect the Second Capacitor
After the battery is removed, we connect an identical uncharged capacitor (C2) in parallel with C1. The total capacitance of the system becomes:
Ctotal=C1+C2=C+C=2C
Hint: When capacitors are connected in parallel, their capacitances add up.
Step 4: Determine the New Voltage
When the uncharged capacitor is connected, the charge (Q) will redistribute between the two capacitors. The total charge remains the same, but the voltage across both capacitors will change. The new voltage (Vc) across the capacitors can be calculated as:
Vc=QtotalCtotal=Q+02C=Q2C
Since Q=CV, we can substitute:
Vc=CV2C=V2
Hint: The voltage across capacitors in parallel is the same, and the total charge is conserved.
Step 5: Calculate the Final Energy
The final energy (Uf) stored in the system after connecting the second capacitor can be calculated as:
Uf=12CtotalV2c=12(2C)(V2)2
Substituting the values:
Uf=12(2C)(V24)=12C⋅V22=14CV2
Hint: The energy is calculated using the new total capacitance and the new voltage after connecting the second capacitor.
Step 6: Compare Initial and Final Energies
Now, we can compare the initial and final energies:
- Initial energy: Ui=12CV2
- Final energy: Uf=14CV2
From this, we can see that:
Uf=12Ui
This means the final energy is half of the initial energy.
Conclusion
Thus, the total electrostatic energy of the resulting system decreases by half when the identical uncharged capacitor is connected in parallel.
Final Answer: The total electrostatic energy of the resulting system is 12Ui.
We have one capacitor (let's call it C1) that is charged by a battery to a voltage V. The charge on this capacitor can be calculated using the formula:
Q=C⋅V
where C is the capacitance of the capacitor.
The electrostatic energy (Ui) stored in the charged capacitor can be calculated using the formula:
Ui=12CV2
After the battery is removed, we connect an identical uncharged capacitor (C2) in parallel with C1. The total capacitance of the system becomes:
Ctotal=C1+C2=C+C=2C
When the uncharged capacitor is connected, the charge (Q) will redistribute between the two capacitors. The total charge remains the same, but the voltage across both capacitors will change. The new voltage (Vc) across the capacitors can be calculated as:
Vc=QtotalCtotal=Q+02C=Q2C
Since Q=CV, we can substitute:
Vc=CV2C=V2
The final energy (Uf) stored in the system after connecting the second capacitor can be calculated as:
Uf=12CtotalV2c=12(2C)(V2)2
Substituting the values:
Uf=12(2C)(V24)=12C⋅V22=14CV2
Now, we can compare the initial and final energies:
- Initial energy: Ui=12CV2
- Final energy: Uf=14CV2
Uf=12Ui
Thus, the total electrostatic energy of the resulting system decreases by half when the identical uncharged capacitor is connected in parallel.
Similar Questions
A capacitor of 60 pF charged to 20 volt. Now battery is removed and then this capacitor is connected to another identical uncharged capacitor. Find heat loss in nJ
View SolutionA capacitor of 60 pF charged to 20 volt. Now battery is removed and then this capacitor is connected to another identical uncharged capacitor. Find heat loss in nJ
View Solution
Knowledge Check
A capacitor of capacitance 700 pF is charged by 100 V battery. The electrostatic energy stored by the capacitor is
A2.5×10−8JB3.5×10−6JC2.5×10−4JD3.5×10−4J
A capacitor is charged with a battery and energy stored is U. After disconnecting battery another capacitor of same capacity is connected in parallel with it. Then energy stored in each capacitor is:
View SolutionA capacitor is charged by a cell of emf E the charging battery is then removed. If an identical capacitor is now inserted in the circuit in parallel with the previous capacitor, the potential difference across the new capacitor is
View SolutionA capacitor is charged using a a battery and energy stored is U. After disconnecting the battery another uncharged capacitor of same capacitance is connected in parallel to the first capacitor. Then loss of energy is equal to
View SolutionA capacitor is charged by connecting a battery across its plates. It stores energy U. Now the battery is disconnected and another identical capacior is connected across it, then the energy stores by both capacitors of the system will be
View SolutionAir filled capacitor is charged by a battery and after charging battery is removed. A slab of dielectric material is inserted in it to fill the space completely . The electric field in the capacitor is
View SolutionA 8uF capacitor C1 is charged to V0=120V. The charging battery is then removed and the capacitor is connected in parallel to an uncharged +4μF capacitor C2.
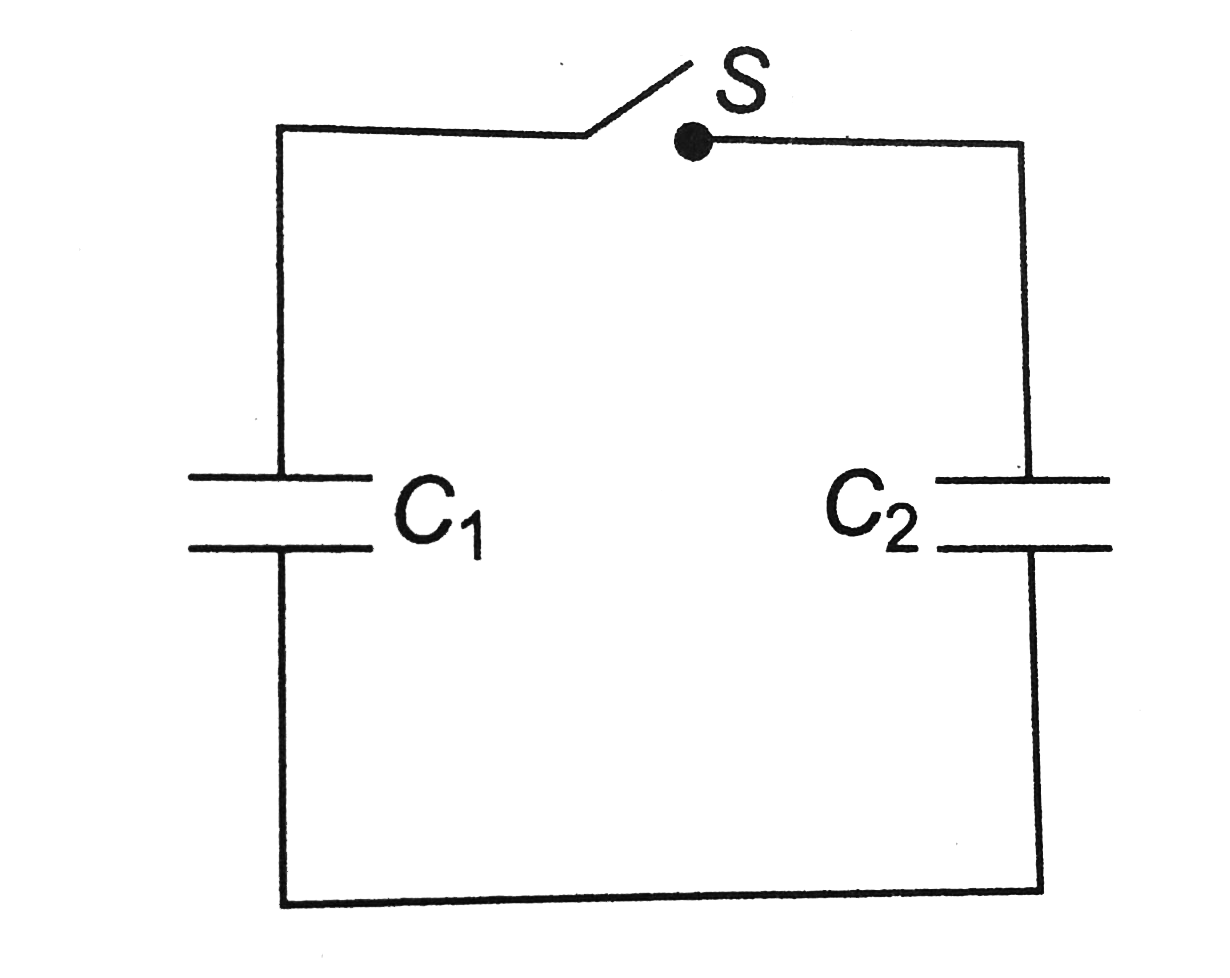
(a) what is the potential difference V across the combination?
(b) what is the stored energy before and after the switch S is closed?
View Solution0.2F capacitor is charged to 600V by a battery. On removing the battery it is connected with another parallel plate condenser of 1F. The potential decreases to
View Solution
