A capacitor is charged with a battery and energy stored is U. After disconnecting battery another capacitor of same capacity is connected in parallel with it. Then energy stored in each capacitor is:
U/2
U/4
4 U
2 U
The correct Answer is:B
To solve the problem, we need to analyze the situation step by step.
Step 1: Initial Energy Stored in the Capacitor
When the capacitor (C) is charged by a battery with voltage (V), the charge (Q) on the capacitor is given by:
Q=C⋅V
The energy (U) stored in the capacitor is given by the formula:
U=12Q2C
Substituting Q into the energy formula:
U=12(C⋅V)2C=12CV2
Step 2: Disconnecting the Battery
After charging, the battery is disconnected. The capacitor now holds charge Q and energy U.
Step 3: Connecting Another Capacitor in Parallel
Now, we connect another capacitor of the same capacitance (C) in parallel with the charged capacitor. When capacitors are connected in parallel, the voltage across both capacitors remains the same, but the total charge gets redistributed.
Step 4: Charge Distribution
The total charge before connecting the second capacitor is Q. After connecting the second capacitor, the total capacitance becomes:
Ctotal=C+C=2C
Since the voltage (V') across both capacitors must be the same, we can use the relationship:
Q=C⋅V
The new voltage across the combined capacitors can be expressed as:
Q=2C⋅V′
Setting the two equations for charge equal gives:
C⋅V=2C⋅V′
From this, we can solve for the new voltage:
V′=V2
Step 5: New Charge on Each Capacitor
The charge on each capacitor after connecting them in parallel will be:
Q′=C⋅V′=C⋅V2=Q2
Thus, each capacitor now has a charge of Q2.
Step 6: New Energy Stored in Each Capacitor
The energy stored in each capacitor can be calculated using the formula:
U′=12(Q′)2C
Substituting Q′=Q2:
U′=12(Q2)2C=12Q24C=Q28C
Step 7: Relating New Energy to Original Energy
Recall that the original energy U was:
U=12Q2C
Now, we can express the new energy stored in each capacitor:
U′=14⋅12Q2C=U4
Conclusion
Thus, the energy stored in each capacitor after connecting the second capacitor in parallel is:
U′=U4
When the capacitor (C) is charged by a battery with voltage (V), the charge (Q) on the capacitor is given by:
Q=C⋅V
The energy (U) stored in the capacitor is given by the formula:
U=12Q2C
Substituting Q into the energy formula:
U=12(C⋅V)2C=12CV2
After charging, the battery is disconnected. The capacitor now holds charge Q and energy U.
Now, we connect another capacitor of the same capacitance (C) in parallel with the charged capacitor. When capacitors are connected in parallel, the voltage across both capacitors remains the same, but the total charge gets redistributed.
The total charge before connecting the second capacitor is Q. After connecting the second capacitor, the total capacitance becomes:
Ctotal=C+C=2C
Since the voltage (V') across both capacitors must be the same, we can use the relationship:
Q=C⋅V
The new voltage across the combined capacitors can be expressed as:
Q=2C⋅V′
Setting the two equations for charge equal gives:
C⋅V=2C⋅V′
From this, we can solve for the new voltage:
V′=V2
The charge on each capacitor after connecting them in parallel will be:
Q′=C⋅V′=C⋅V2=Q2
Thus, each capacitor now has a charge of Q2.
The energy stored in each capacitor can be calculated using the formula:
U′=12(Q′)2C
Substituting Q′=Q2:
U′=12(Q2)2C=12Q24C=Q28C
Recall that the original energy U was:
U=12Q2C
Now, we can express the new energy stored in each capacitor:
U′=14⋅12Q2C=U4
Thus, the energy stored in each capacitor after connecting the second capacitor in parallel is:
U′=U4
Similar Questions
The energy stored in 4μF capacitors is
View SolutionA capacitor is charged using a a battery and energy stored is U. After disconnecting the battery another uncharged capacitor of same capacitance is connected in parallel to the first capacitor. Then loss of energy is equal to
View SolutionThe capacitors shown in figure. Is in steady state. The energy stored in the capacitor is
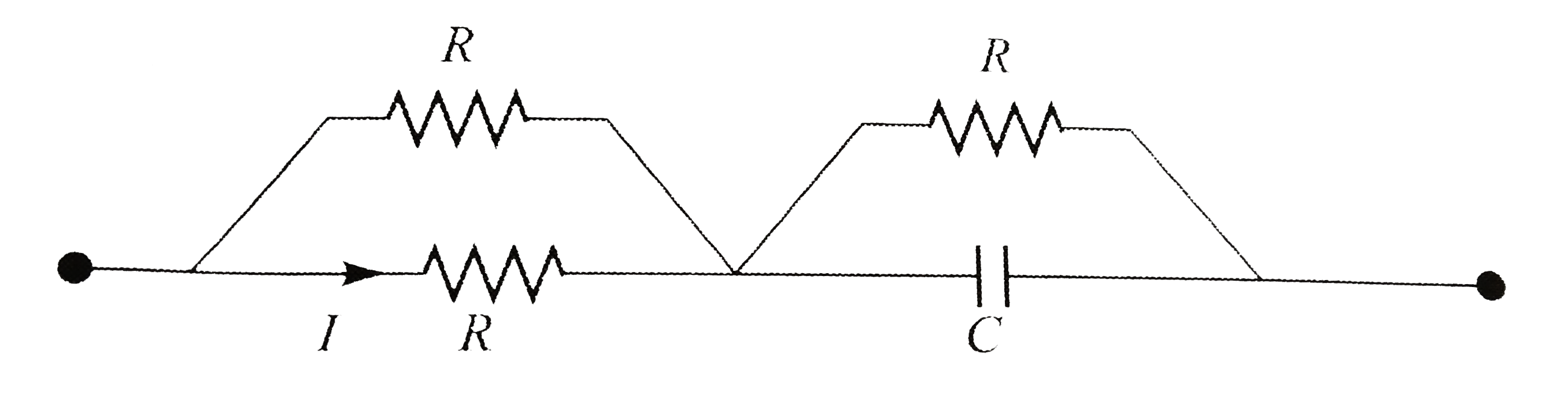 View Solution
View SolutionA capacitor is charged by a battery. The battery is removed and another identical uncharged capacitor is connected in parallel. The total electrostatic energy of resulting system:
View SolutionA capacitor is charged by connecting a battery across its plates. It stores energy U. Now the battery is disconnected and another identical capacior is connected across it, then the energy stores by both capacitors of the system will be
View SolutionWhat happens to the energy stored in a capacitor if after disconnecting the battery, the plates of a charged capacitor are moved farther
View SolutionA capacitor is charge until it stores an energy of 1J. A second uncharged capacitor is connected to it, so that charge districutes equally. The final energy stored in the second capacitor is
View SolutionA capacitor C is fully charged with voltage V0. After disconnecting the voltage source, it is connected in parallel with another uncharged capacitor of capacitance C2. The energy loss in the process after the charge is distributed between the two capacitors is :
View SolutionA 100μF capacitor is charged to 100V. After the charging, battery is disconnected. The capacitor is then connected in parallel to another capacitor. The final voltage is 20V. Calculate the capacity of second capacitor.
View SolutionThe energy stored in the capacitor in the steady state is
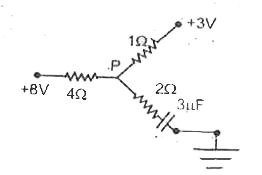 View Solution
View Solution


