The point charges +q,−2q and +q are placed at point (x=0,y=a,z=0),(x=0,y=0,z=0) and (x=a,y=0,z=0), repectively. The magnitude and direction of the electric dipole moment vector of this charge assembly are
√2qa along +y direction
√2aq along the line joining points (x=0,y=0,z=0) and (x=a,y=a,z=0)
qa along the line joining points (x=0,y=0,z=0) and (x=a,y=a,z=0)
√2 aq along +x direction
The correct Answer is:B
To find the electric dipole moment vector of the charge assembly consisting of point charges +q, −2q, and +q located at the specified coordinates, we can follow these steps:
Step 1: Identify the positions of the charges
- The charges are located at:
- Charge +q at (0,a,0)
- Charge −2q at (0,0,0)
- Charge +q at (a,0,0)
Step 2: Calculate the dipole moment for each charge
The electric dipole moment →p for a point charge is given by:
→p=q⋅→r
where →r is the position vector of the charge from the origin.
1. For charge +q at (0,a,0):
→p1=+q⋅(0,a,0)=(0,qa,0)
2. For charge −2q at (0,0,0):
→p2=−2q⋅(0,0,0)=(0,0,0)
3. For charge +q at (a,0,0):
→p3=+q⋅(a,0,0)=(qa,0,0)
Step 3: Sum the dipole moments
The total dipole moment →ptotal is the vector sum of the individual dipole moments:
→ptotal=→p1+→p2+→p3
Substituting the values:
→ptotal=(0,qa,0)+(0,0,0)+(qa,0,0)=(qa,qa,0)
Step 4: Calculate the magnitude of the dipole moment
The magnitude of the dipole moment vector is given by:
|→ptotal|=√(qa)2+(qa)2=√2(qa)2=qa√2
Step 5: Determine the direction of the dipole moment
The direction of the dipole moment vector →ptotal=(qa,qa,0) can be expressed in terms of its components. It points in the direction of the vector from the origin towards the point (qa,qa,0).
Final Answer
The magnitude and direction of the electric dipole moment vector of this charge assembly is:
|→p|=qa√2along the line joining (0,0,0) to (a,a,0).
- The charges are located at:
- Charge +q at (0,a,0)
- Charge −2q at (0,0,0)
- Charge +q at (a,0,0)
The electric dipole moment →p for a point charge is given by:
→p=q⋅→r
where →r is the position vector of the charge from the origin.
→p1=+q⋅(0,a,0)=(0,qa,0)
→p2=−2q⋅(0,0,0)=(0,0,0)
→p3=+q⋅(a,0,0)=(qa,0,0)
The total dipole moment →ptotal is the vector sum of the individual dipole moments:
→ptotal=→p1+→p2+→p3
Substituting the values:
→ptotal=(0,qa,0)+(0,0,0)+(qa,0,0)=(qa,qa,0)
The magnitude of the dipole moment vector is given by:
|→ptotal|=√(qa)2+(qa)2=√2(qa)2=qa√2
The direction of the dipole moment vector →ptotal=(qa,qa,0) can be expressed in terms of its components. It points in the direction of the vector from the origin towards the point (qa,qa,0).
The magnitude and direction of the electric dipole moment vector of this charge assembly is:
|→p|=qa√2along the line joining (0,0,0) to (a,a,0).
Similar Questions
What is the locus of a point (x,y,z) for which y=0,z=0?
View SolutionWhat is the locus of a point (x,y,z) for which y=0,z=0?
View SolutionThree charged particles having charges q, -2q & q are placed in a line at points (-a, 0), (0,0) & (a , 0) respectively. The expression for electric potential at P(r, 0 ) for r >> a is
View SolutionTwo point charges −q and +q are located at points (0,0−a) and (0,0,a) respectively. The electric potential at point (0,0,z)is (Z>a)
View Solutionfor every point (x,y,z) on the y-axis: (A) x=0,y=0 (B) x=0,z=0 (C) y=0,z=0 (D) y≠0,x=0,z=0
View SolutionFour charges +q,+q−q, and -q are placed on X - Y plane at the points whose coordinates are (0.5,0),(0,0.5),(−0.5,0)and(0,−0.5) respectively.
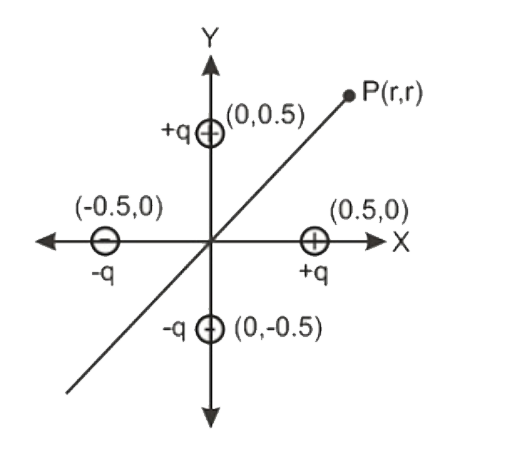
The electric field due to these charges at a point P(r,r), where r>>0.5, will be
View SolutionWhat is the locus of a point for which
(i) x=0,y=0
(ii) y=0,z=0
(iii) z=0,x=0
(iv)x=a,y=b
(v) y=b,z=0
(vi)z=c,x=a ?
View SolutionFor every point P(x, y, z) on the xy-plane, a. x=0 b. y=0 c. z=0 d. x=y=z=0
View SolutionFor every point P(x, y, z) on the xy-plane, a. x=0 b. y=0 c. z=0 d. x=y=z=0
View SolutionThe planes 2x + 5y + 3z = 0, x-y+4z = 2 and7y-5z + 4 = 0
View Solution
