Three charged particles having charges q, -2q & q are placed in a line at points (-a, 0), (0,0) & (a , 0) respectively. The expression for electric potential at P(r, 0 ) for r >> a is
14πε0qa2r4
14πε02qa2r3
14πε04qa2r2
14πε08qa2r
The correct Answer is:B
To find the expression for the electric potential at point P(r, 0) due to the three charged particles with charges q,−2q, and q located at points (−a,0),(0,0), and (a,0) respectively, we will follow these steps:
Step 1: Write the formula for electric potential
The electric potential V due to a point charge Q at a distance r is given by the formula:
V=kQr
where k is Coulomb's constant, k=14πϵ0.
Step 2: Calculate the distance from each charge to point P
For point P located at (r,0):
- The distance from charge q at (−a,0) to point P is:
d1=r+a
- The distance from charge −2q at (0,0) to point P is:
d2=r
- The distance from charge q at (a,0) to point P is:
d3=r−a
Step 3: Write the potentials due to each charge
Now we can express the potential at point P due to each charge:
1. Due to charge q at (−a,0):
V1=kqr+a
2. Due to charge −2q at (0,0):
V2=−2kqr
3. Due to charge q at (a,0):
V3=kqr−a
Step 4: Calculate the total potential at point P
The total electric potential V at point P is the sum of the potentials due to all three charges:
V=V1+V2+V3
Substituting the expressions we found:
V=kqr+a−2kqr+kqr−a
Step 5: Simplify the expression
To simplify this expression, we need to find a common denominator, which is (r+a)(r)(r−a):
V=kq(r(r−a)+(−2)(r+a)(r−a)+(r+a)r(r+a)(r)(r−a))
After simplification and using the approximation r≫a, we can neglect terms involving a in the denominator.
Step 6: Final expression
After performing the algebra and simplifying, we arrive at:
V≈2kqa2r3
Thus, the expression for the electric potential at point P when r≫a is:
V≈2kqa2r3
The electric potential V due to a point charge Q at a distance r is given by the formula:
V=kQr
where k is Coulomb's constant, k=14πϵ0.
For point P located at (r,0):
- The distance from charge q at (−a,0) to point P is:
d1=r+a
- The distance from charge −2q at (0,0) to point P is:
d2=r
- The distance from charge q at (a,0) to point P is:
d3=r−a
Now we can express the potential at point P due to each charge:
1. Due to charge q at (−a,0):
V1=kqr+a
2. Due to charge −2q at (0,0):
V2=−2kqr
3. Due to charge q at (a,0):
V3=kqr−a
The total electric potential V at point P is the sum of the potentials due to all three charges:
V=V1+V2+V3
Substituting the expressions we found:
V=kqr+a−2kqr+kqr−a
To simplify this expression, we need to find a common denominator, which is (r+a)(r)(r−a):
V=kq(r(r−a)+(−2)(r+a)(r−a)+(r+a)r(r+a)(r)(r−a))
After simplification and using the approximation r≫a, we can neglect terms involving a in the denominator.
After performing the algebra and simplifying, we arrive at:
V≈2kqa2r3
Thus, the expression for the electric potential at point P when r≫a is:
V≈2kqa2r3
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - C
53 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - D
9 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - A
44 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
15 Videos
Similar Questions
Two point charges −q and +q are located at points (0,0−a) and (0,0,a) respectively. The electric potential at point (0,0,z)is (Z>a)
View SolutionThree point charge q1=1μC,q2=−2μC and q3=3μC are placed at (1m,0,0),(0,2m,0) and (0,0,3m) respectively. Find the electric potential at as origin.
View SolutionTwo point charges q and –q are at positions (0,0,d) and (0,0, –d) respectively . What is the electric field at (a,0,0 ) ?
View SolutionTwo point charges q and –q are at positions (0,0,d) and (0,0, –d) respectively . What is the electric field at (a,0,0 ) ?
View SolutionTwo fixed charges −2Q and +Q are located at points (−3a,0) and (+3a,0) respectively. Then which of the following statement is correct?
View SolutionTwo charges q1andq2 are placed at (0,0,d) and (0,0,-d) respectively. Find locus of points where the potential is zero.
View SolutionTwo point charges +q and -q are held fixed at (−a,0) and (a,0) respectively of a x-y coordinate system then
View SolutionAlong the x-axis, three charges q2,−q and q2 are placed at x=0,x=a and x=2a respectively. The resultant electric potential at a point P located at a distance r from the charge −q, (r>>a) is : ( ε0 is the permittivity of free space)
View SolutionFour charges +q,+q−q, and -q are placed on X - Y plane at the points whose coordinates are (0.5,0),(0,0.5),(−0.5,0)and(0,−0.5) respectively.
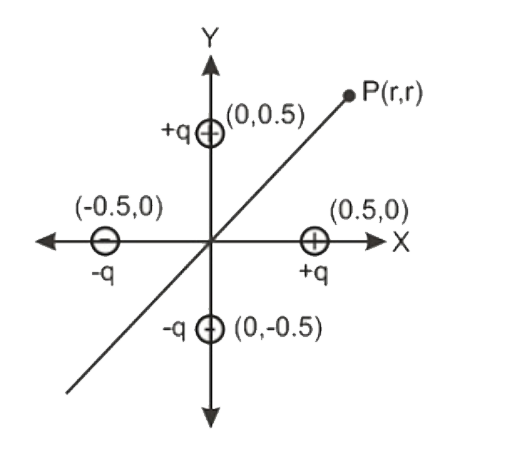
The electric field due to these charges at a point P(r,r), where r>>0.5, will be
View SolutionThe point charges +q,−2q and +q are placed at point (x=0,y=a,z=0),(x=0,y=0,z=0) and (x=a,y=0,z=0), repectively. The magnitude and direction of the electric dipole moment vector of this charge assembly are
View Solution
