A potentiometer wire of Length L and a resistance r are connected in series with a battery of e.m.f. E0 and a resistance r1. An unknown e.m.f. E is balanced at a length l of the potentiometer wire. The e.m.f. E will be given by :
LE0rlir1
E0r(r+r1).lL
E0lL
LE0r(r+r1)l
The correct Answer is:B
To solve the problem, we will follow these steps:
Step 1: Understand the Circuit
We have a potentiometer wire of length L and resistance r connected in series with a battery of e.m.f. E0 and a resistance r1. An unknown e.m.f. E is balanced at a length l of the potentiometer wire.
Step 2: Find the Current in the Circuit
The total resistance in the circuit is the sum of the resistance of the potentiometer wire and the external resistance:
Rtotal=r+r1
Using Ohm's law, the current I flowing through the circuit can be calculated as:
I=E0Rtotal=E0r+r1
Step 3: Calculate the Potential Difference Across the Potentiometer Wire
The potential difference VAB across the potentiometer wire can be calculated using:
VAB=I⋅r
Substituting the expression for I:
VAB=(E0r+r1)⋅r
Step 4: Determine the Potential Gradient
The potential gradient K along the potentiometer wire is given by:
K=VABL
Substituting the expression for VAB:
K=(E0⋅rr+r1)L=E0⋅rL⋅(r+r1)
Step 5: Calculate the Unknown E.m.f. E
The e.m.f. E that corresponds to the balanced length l can be expressed as:
E=K⋅l
Substituting the expression for K:
E=(E0⋅rL⋅(r+r1))⋅l
Final Expression
Thus, the unknown e.m.f. E is given by:
E=E0⋅r⋅lL⋅(r+r1)
We have a potentiometer wire of length L and resistance r connected in series with a battery of e.m.f. E0 and a resistance r1. An unknown e.m.f. E is balanced at a length l of the potentiometer wire.
The total resistance in the circuit is the sum of the resistance of the potentiometer wire and the external resistance:
Rtotal=r+r1
Using Ohm's law, the current I flowing through the circuit can be calculated as:
I=E0Rtotal=E0r+r1
The potential difference VAB across the potentiometer wire can be calculated using:
VAB=I⋅r
Substituting the expression for I:
VAB=(E0r+r1)⋅r
The potential gradient K along the potentiometer wire is given by:
K=VABL
Substituting the expression for VAB:
K=(E0⋅rr+r1)L=E0⋅rL⋅(r+r1)
The e.m.f. E that corresponds to the balanced length l can be expressed as:
E=K⋅l
Substituting the expression for K:
E=(E0⋅rL⋅(r+r1))⋅l
Thus, the unknown e.m.f. E is given by:
E=E0⋅r⋅lL⋅(r+r1)
Similar Questions
A potentiometer wire of length 100 cm has a resistance of 10Ω. It is connected in series with a resistance R and cell of emf 2V and negligible resistance. A source of emf 10 mV is balanced against a length of 40cm of the potentiometer wire. What is the value of R?
View SolutionAB is a potentiometer wire of length 100cm and its resistance is 10ohm. It is connected in series with a resistance R=40 ohm and a battery of e.m.f. wV and negigible internal resistance. If a source of unknown e.m.f. E is balanced by 40cm length of the potentiometer wire, the value of E is:

View Solution
Knowledge Check
A potentiometer wire of length 100 cm has a resistance of 100Ω it is connected in series with a resistance and a battery of emf 2 V and of negligible internal resistance. A source of emf 10 mV is balanced against a length of 40 cm of the potentiometer wire. what is the value of the external resistance?
A790ΩB890ΩC990ΩD1090ΩA potentiometer wire of length 100cm has a resistance of 10Ω. It is connected in series with a resistance and a cell of emf 2V and of negligible interal resistance. A source of emf 10mV is balanced against a length of 40cm of the potentiometer wire. What is the value of external resistance?
A790ΩB890ΩC990ΩD1090Ω
A potentiometer wire of length 1m and resistance 20Ω is connected in series with a 15V battery and an external resistance 40Ω . A secondary cell of emf E in the secondary circuit is balanced by 24 cm long potentiometer wire. The emf E of the cell is ,
View SolutionA potentiometer wire of length 10m and resistance 30 ohm is connected in series with a battery of emf 2.5V, internal resistance 5 ohm and external resistance R. If the fall of potential along the potentiometer wire is 50mV/m, the value of R is ohms is
View SolutionA potentiometer wire of length 10m and resistance 30Ω is connected in series with a battery of emf 2.5V, internal resistance 5Ω and an external resistance R. If the fall of potential along the potentiometer wire is 50μVmm−1, then the value of R is found to be 23nΩ. What is n?
View SolutionA potentiometer wire of length 100cm having a resistance of 10Ω is connected in series with a resistance R and a cell of emf 2V of negligible internal resistance. A source of emf

of 10mV is balanced against a length of 40cm of the potentiometer wire. What is the value of resistance R ?
View SolutionA potentiometer wire of length 100cm having a resistance of 10Ω is connected in series with a resistance R and a cell of emf 2V of negligible internal resistance. A source of emf

of 10mV is balanced against a length of 40cm of the potentiometer wire. What is the value of resistance R ?
View SolutionThe potentiometer wire of length 100cm has a resistance of 10Ω. It is connected in series with a resistance of 5Ω and an accumulaot or emf 3V having negligible resistance. A source 1.2V is balanced against a length 'L' of the potentionmeter wire. find the value of L.
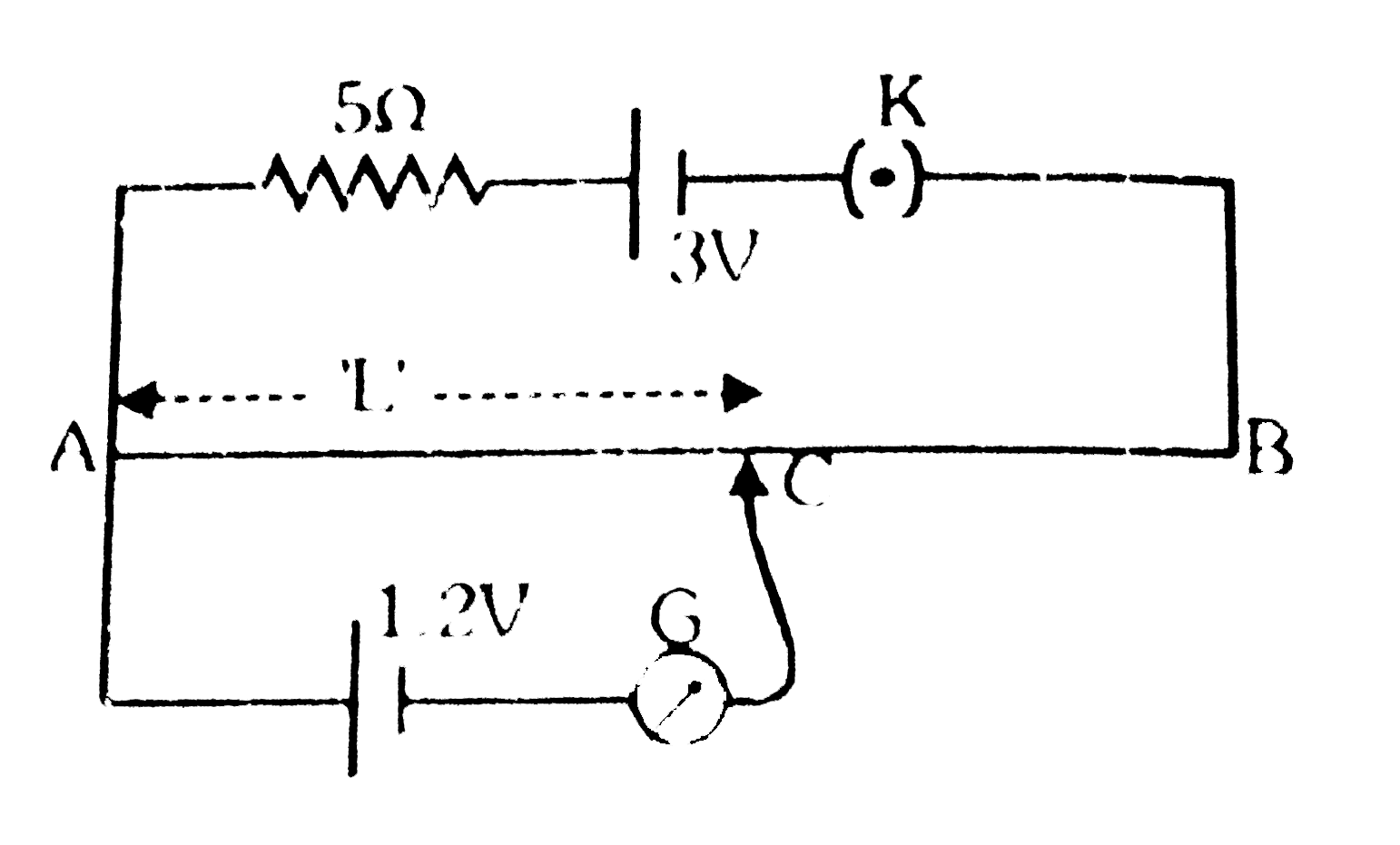
View Solution
