A potentiometer wire of length 1m and resistance 20Ω is connected in series with a 15V battery and an external resistance 40Ω . A secondary cell of emf E in the secondary circuit is balanced by 24 cm long potentiometer wire. The emf E of the cell is ,
2.5V
1.2V
2.0V
3 V
To solve the problem step by step, we will follow the given information and apply the relevant formulas.
Step 1: Determine the total resistance in the circuit
The total resistance Rtotal in the circuit is the sum of the resistance of the potentiometer wire and the external resistance.
Rtotal=Rpotentiometer+Rexternal=20Ω+40Ω=60Ω
Hint: Remember that resistances in series simply add up.
Step 2: Calculate the current flowing through the circuit
Using Ohm's Law, the current I in the circuit can be calculated using the formula:
I=VRtotal=15V60Ω=14A=0.25A
Hint: Ohm's Law states that V=I×R.
Step 3: Calculate the potential gradient (K) across the potentiometer wire
The potential gradient K is defined as the voltage drop per unit length of the wire. The voltage drop across the potentiometer wire can be calculated as:
Vpotentiometer=I×Rpotentiometer=0.25A×20Ω=5V
Now, the potential gradient K is given by:
K=VpotentiometerL=5V1m=5V/m
Hint: The potential gradient tells you how much voltage drops per meter of wire.
Step 4: Calculate the EMF of the secondary cell
The EMF E of the secondary cell is determined by the potential gradient and the length of the wire that balances the cell. Given that the balancing length is 24 cm (or 0.24 m), we can find E:
E=K×balancing length=5V/m×0.24m=1.2V
Hint: The balancing length is crucial for determining the EMF of the cell.
Final Answer
The EMF E of the secondary cell is 1.2 V.
---
The total resistance Rtotal in the circuit is the sum of the resistance of the potentiometer wire and the external resistance.
Using Ohm's Law, the current I in the circuit can be calculated using the formula:
The potential gradient K is defined as the voltage drop per unit length of the wire. The voltage drop across the potentiometer wire can be calculated as:
The EMF E of the secondary cell is determined by the potential gradient and the length of the wire that balances the cell. Given that the balancing length is 24 cm (or 0.24 m), we can find E:
The EMF E of the secondary cell is 1.2 V.
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-1 DAILY TUTORIAL SHEET-415videos
DC CIRCUIT
- BOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-1 DAILY TUTORIAL SHEET -515videos
DC CIRCUIT
- BOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-1 DAILY TUTORIAL SHEET-215videos
DC CIRCUIT
- BOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - IN-CHAPTER EXERCISE-F10videos
CURRENT ELECTRICITY
- BOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )31videos
DYNAMICS OF A PARTICLE
Similar Questions
A potentiometer wire of length 10m and resistance 30Ω is connected in series with a battery of emf 2.5V, internal resistance 5Ω and an external resistance R. If the fall of potential along the potentiometer wire is 50μVmm−1, then the value of R is found to be 23nΩ. What is n?
View SolutionA potentiometer wire of length 1 m has a resistance of 10Ω. It is connected to a 6V battery in series with a resistance of 5Ω. Determine the emf of the primary cell which gives a balance point at 40cm.
View Solution
Knowledge Check
- Question 1 - Select One
A potentiometer wire of length 100cm has a resistance of 10Ω. It is connected in series with a resistance and a cell of emf 2V and of negligible interal resistance. A source of emf 10mV is balanced against a length of 40cm of the potentiometer wire. What is the value of external resistance?
A790ΩB890ΩC990ΩD1090Ω - Question 2 - Select One
A potentiometer wire of length 100 cm has a resistance of 100Ω it is connected in series with a resistance and a battery of emf 2 V and of negligible internal resistance. A source of emf 10 mV is balanced against a length of 40 cm of the potentiometer wire. what is the value of the external resistance?
A790ΩB890ΩC990ΩD1090Ω
A potentiometer wire of length 100cm having a resistance of 10Ω is connected in series with a resistance R and a cell of emf 2V of negligible internal resistance. A source of emf

of 10mV is balanced against a length of 40cm of the potentiometer wire. What is the value of resistance R ?View SolutionA potentiometer wire of length 100cm having a resistance of 10Ω is connected in series with a resistance R and a cell of emf 2V of negligible internal resistance. A source of emf

of 10mV is balanced against a length of 40cm of the potentiometer wire. What is the value of resistance R ?View SolutionA potentiometer wire of length 10m and resistance 30 ohm is connected in series with a battery of emf 2.5V, internal resistance 5 ohm and external resistance R. If the fall of potential along the potentiometer wire is 50mV/m, the value of R is ohms is
View SolutionAB is a potentiometer wire of length 100 cm and its resistance is 10Ω. It is connected in series with a resistance R = 40 Ω and a battery of emf 2 V and negligible internal resistance. If a source of unknown emf E is balanced by 40 cm length of the potentiometer wire, the value of E is
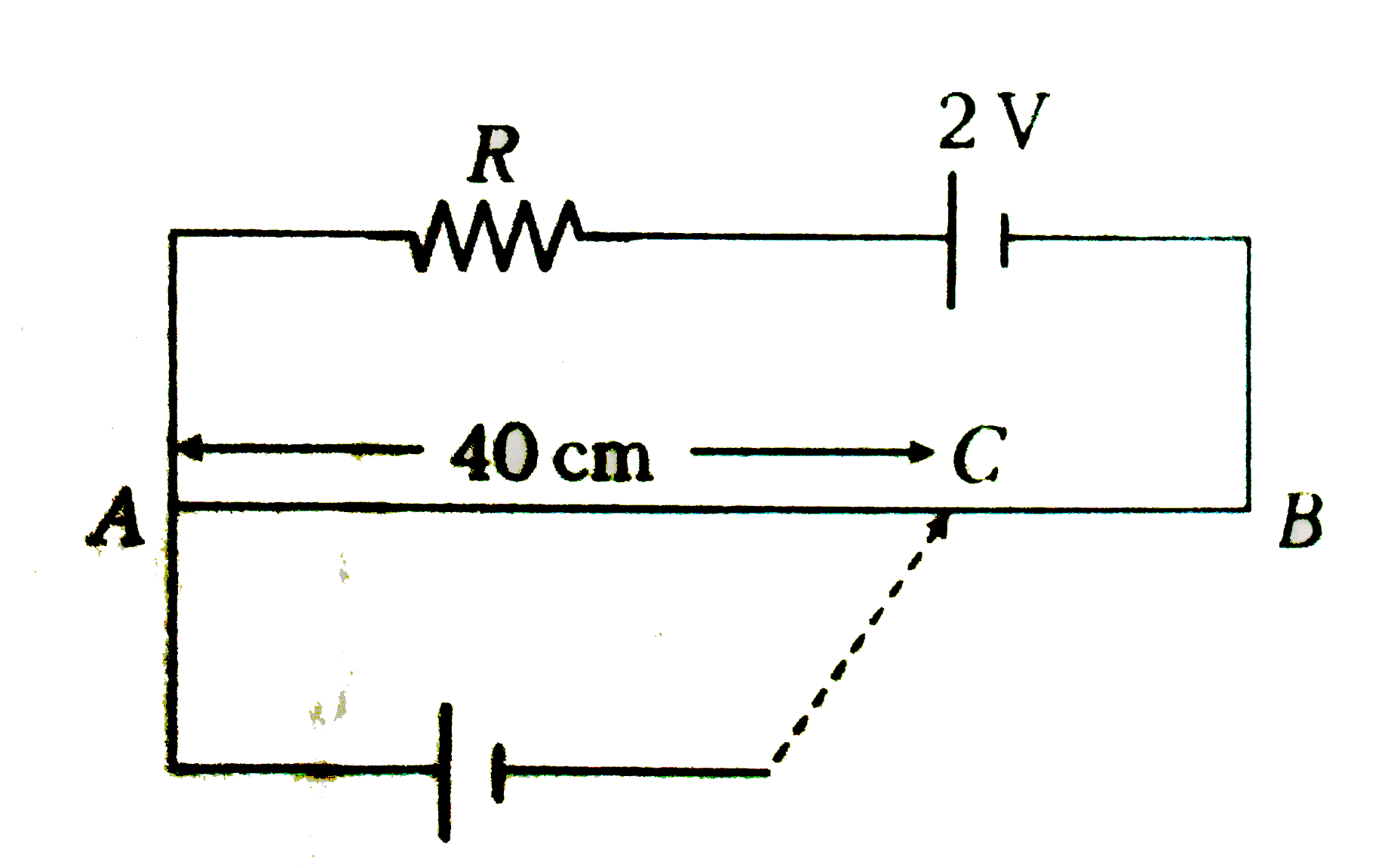 View Solution
View SolutionAB is a potentiometer wire of length 100cm and its resistance is 10ohm. It is connected in series with a resistance R=40 ohm and a battery of e.m.f. wV and negigible internal resistance. If a source of unknown e.m.f. E is balanced by 40cm length of the potentiometer wire, the value of E is:
 View Solution
View SolutionA potentiometer wire of length 100 cm has a resistance of 10Ω. It is connected in series with a resistance R and cell of emf 2V and negligible resistance. A source of emf 10 mV is balanced against a length of 40cm of the potentiometer wire. What is the value of R?
View Solution

