Resistance n, each of rohm, when connected in parallel give an equivalent resistance of Rohm. If these resistances were connected series, the combination would have a resistance in ohm, equal to
n2R
Rn2
Rn
nR
The correct Answer is:A
To solve the problem, we need to find the equivalent resistance when n resistors, each of resistance rohm, are connected in series after knowing their equivalent resistance when connected in parallel.
1. Understanding Parallel Resistance:
When n resistors of resistance r are connected in parallel, the formula for equivalent resistance \( R \) is given by:
\(
\frac{1}{R} = \frac{1}{r} + \frac{1}{r} + \ldots + \frac{1}{r} \quad (n \text{ times})
\)
This simplifies to:
\(
\frac{1}{R} = \frac{n}{r}
\)
Therefore, we can express \( R \) as:
\(
R = \frac{r}{n}
\)
2. Finding the Value of r:
From the equation \( R = \frac{r}{n} \), we can rearrange it to find \( r \):
\(
r = R \cdot n
\)
3. Understanding Series Resistance:
When the same n resistors are connected in series, the equivalent resistance \( R_s \) is given by:
\(
R_s = r + r + r + \ldots + r \quad (n \text{ times})
\)
This simplifies to:
\(
R_s = n \cdot r
\)
4. Substituting the Value of r:
Now, we substitute the value of \( r \) we found earlier:
\(
R_s = n \cdot (R \cdot n) = n^2 \cdot R
\)
5. Final Result:
Thus, the equivalent resistance when n resistors of resistance r are connected in series is:
\(
R_s = n^2 R
\)
Final Answer:
The equivalent resistance when n resistors of rohm each are connected in series is \( n^2 R \).
When n resistors of resistance r are connected in parallel, the formula for equivalent resistance \( R \) is given by:
\(
\frac{1}{R} = \frac{1}{r} + \frac{1}{r} + \ldots + \frac{1}{r} \quad (n \text{ times})
\)
This simplifies to:
\(
\frac{1}{R} = \frac{n}{r}
\)
Therefore, we can express \( R \) as:
\(
R = \frac{r}{n}
\)
From the equation \( R = \frac{r}{n} \), we can rearrange it to find \( r \):
\(
r = R \cdot n
\)
When the same n resistors are connected in series, the equivalent resistance \( R_s \) is given by:
\(
R_s = r + r + r + \ldots + r \quad (n \text{ times})
\)
This simplifies to:
\(
R_s = n \cdot r
\)
Now, we substitute the value of \( r \) we found earlier:
\(
R_s = n \cdot (R \cdot n) = n^2 \cdot R
\)
Thus, the equivalent resistance when n resistors of resistance r are connected in series is:
\(
R_s = n^2 R
\)
The equivalent resistance when n resistors of rohm each are connected in series is \( n^2 R \).
Similar Questions
Knowledge Check
Equivalent resistance (in ohm) of the given network is
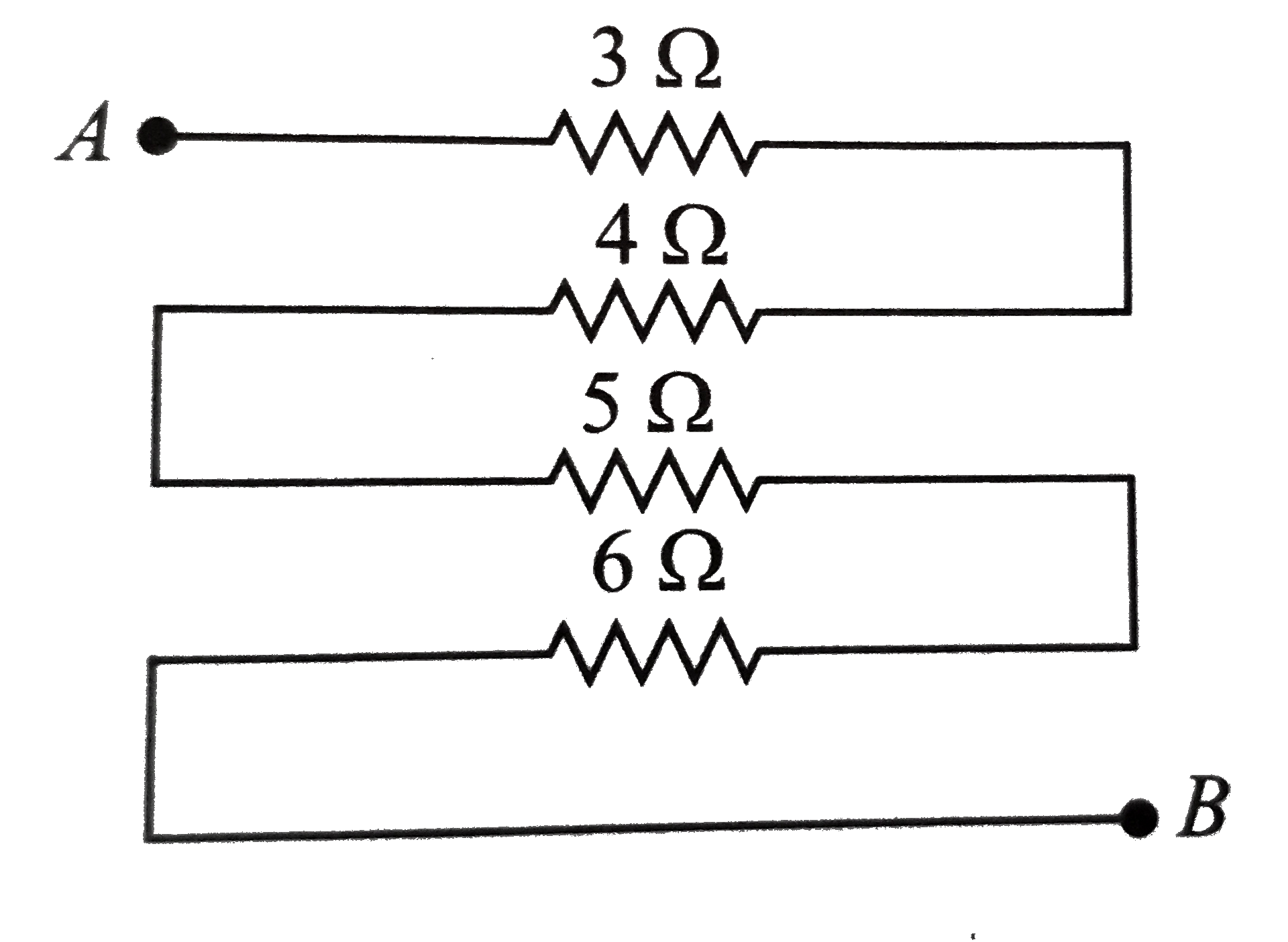 A28B18C26D25
A28B18C26D25Five equal resistances each of value R are connected in a form shown alongside. The equivalent resistance of the network
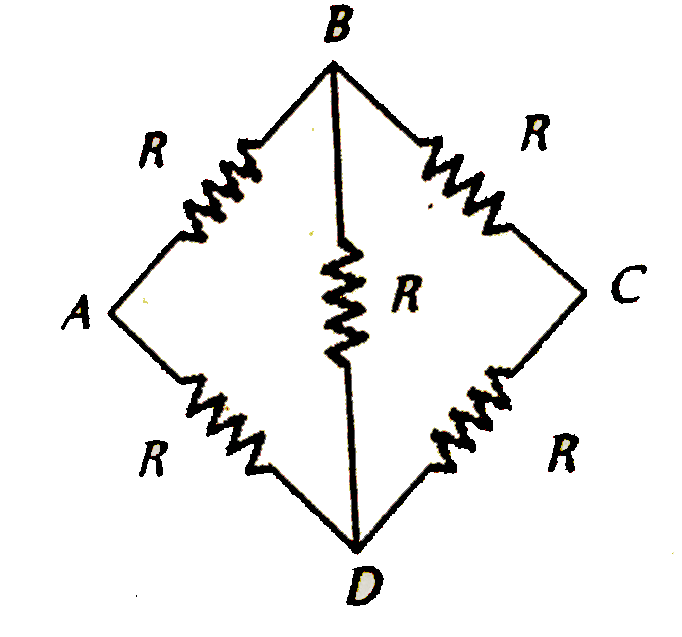 A12RB2RC58RD85R
A12RB2RC58RD85R
A set of n identical resistors, each of resistance RΩ, when connected in series have an effective resistance XΩ and when the resistors are connected in parallel, their effective resistance is YΩ. Find the relation between R, X and Y.
View SolutionThree equal resistance each of 3Ω are in series and connected to cell of internal resistance one ohm. If three resistances are parallel and connected to the same cell. Then the ratio of the respective currents through the electric circuits in the two cases is
View SolutionFive equal resistance each of value R are connected in a circuit . Find equivalent resistance of the network between points A and C

View SolutionSix resistors each of 10 ohm are connected shown. The equivalent resistance between points X and Y is
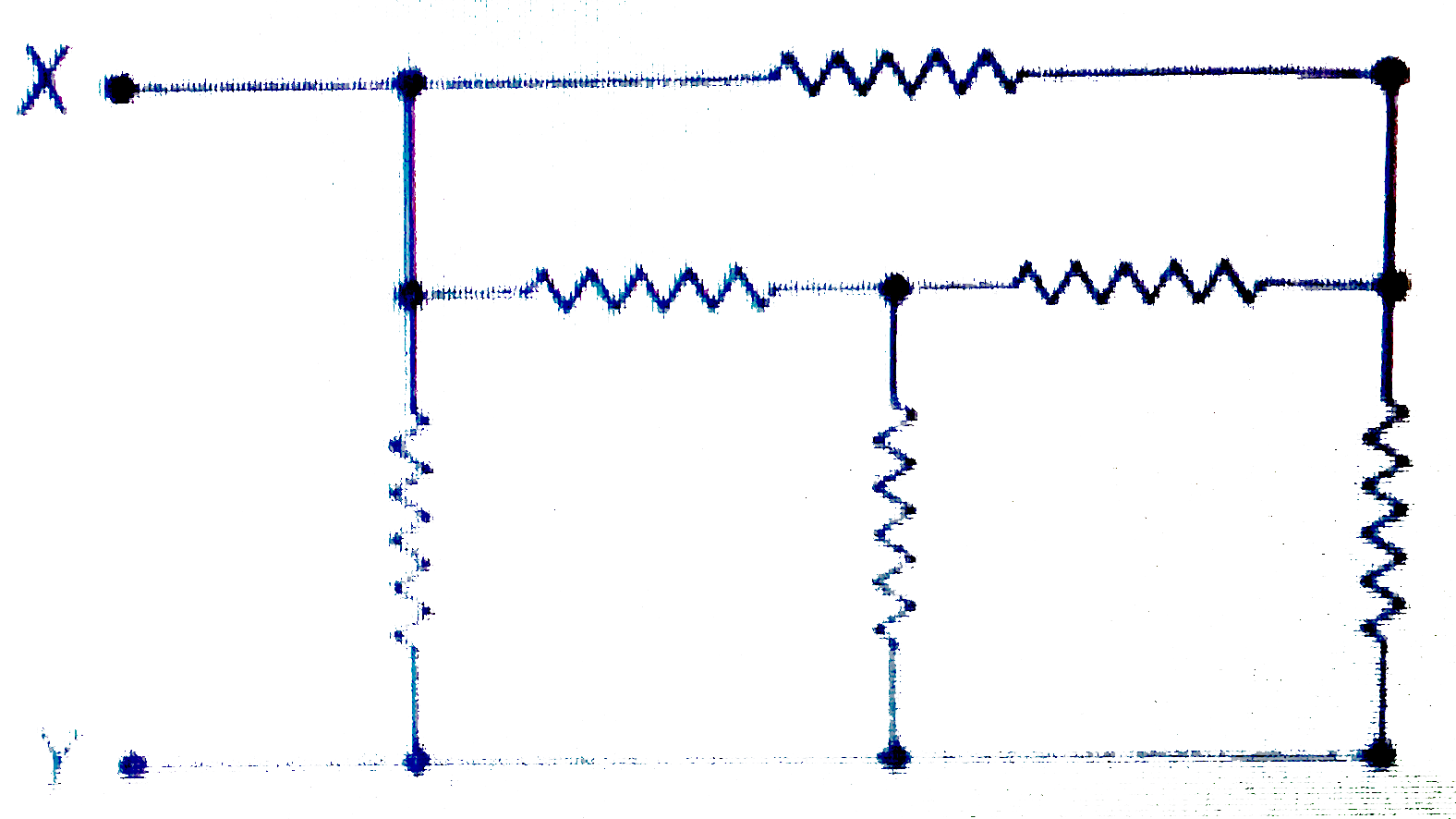
View SolutionThree wires each have resistance 2Ω, if we connect 2 in series with one parallel to the combination the equivalent resistance is
View SolutionA wire of resistance R is divided in 10 equal parts. These parts are connected in parallel, the equivalent resistance of such connection will be
View Solution